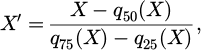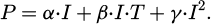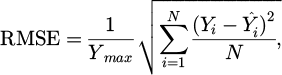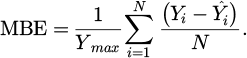| Issue |
EPJ Photovolt.
Volume 15, 2024
|
|
|---|---|---|
| Article Number | 27 | |
| Number of page(s) | 9 | |
| DOI | https://doi.org/10.1051/epjpv/2024023 | |
| Published online | 13 August 2024 | |
https://doi.org/10.1051/epjpv/2024023
Review
Benchmarking photovoltaic plant performance: a machine learning model using multi-dimensional neighbouring plants
1
Green Power Monitor a DNV company, Gran Via de les Corts Catalanes 130, Barcelona, Spain
2
DNV Denmark, Tuborg Parkvej 8, Hellerup, Denmark
* e-mail: gaetana.anamiati@dnv.com
Received:
30
November
2023
Accepted:
4
July
2024
Published online: 13 August 2024
The goal of this study is to monitor the performance of a photovoltaic plant by comparing its power output against others with similar characteristics, referred to as neighbours. The purpose of the 15 neighbours is to have the best reference for the performance of the plant in question, in other words, how the plant under analysis performs compared to the 15 neighbours. A machine learning model based on a feed forward Neural Network was employed to model power production as a function of environmental signals and the sun's position. Here, the data from the neighbours are used to train the model and the data from the plant under analysis are used to evaluate the model and predict the power output. Once the power is predicted, the performance ratio of the plant is calculated. The procedure has been tested and validated at several plants for three different cases and the numerical results highlight how the model is able to identify under/over performing plants. Therefore the developed strategy provides industries a valid tool on the correct functioning of a plant.
Key words: Solar energy / photovoltaic plants / performance / machine learning
© G. Anamiati et al., Published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
In recent years, there has been a growing demand for sustainable energy, with solar photovoltaic (PV) plants gaining popularity due to their numerous advantages. The installed capacity of solar power plants has seen significant growth, increasing from 1 GW in 2004 to approximately 250 GW in 2022, with projections anticipating a global installation of about 500 GW per year by 2040 and a cumulative solar photovoltaic capacity of 8.8 TW by 2050 [1]. Despite this, the performance of PV plants remains an area requiring thorough investigation within the field of Science and Engineering.
The production of electricity directly from sunlight is influenced by a number of climatic and environmental factors (solar radiation, wind speed, ambient temperature, etc.), which have an impact on the power generated by a photovoltaic panel [2–4]. Understanding the performance of a PV plant in advance is crucial for the reliability and stability of energy systems. With modern PV plants equipped with monitoring systems collecting data on system performance and weather conditions, the use of Machine Learning, Data Science, and Artificial Intelligence techniques has gained popularity in predicting power generation. Numerous studies have explored different scenarios in the field of PV power plant forecasting. Mellit et al. [5] employ two ANNs for use in cloudy and sunny days respectively with Irradiance and Temperature as inputs to predict the PV plant. Graditi et al. [6] compare different models that estimates the power production of a PV plant. In details, a phenomenological model proposed by Sandia National Laboratories and two statistical learning models, a Multi-Layer Perceptron (MLP) Neural Network and a Regression approach, are compared. They highlight that more accurate predictions can be obtained by Regression and MLP models as compared to the classical reference method and how more practical they are in terms of required input data and parameters.
Leva et al. [7] use a model based on ANN accompanied by clear sky model for input data validation for next-day energy forecasting of a PV plant with the aim to evaluate its sensitivity. They also introduce different error in order to evaluate the results. Liu et al. [8] propose a back propagation (BP) neural network model. After a correlation analysis, they consider the following parameters as inputs of the model: hourly solar radiation intensity, the highest, the lowest daily and the average daily temperature, and hourly power output of the PV system. The output of the model is the forecasted PV power 24 hours ahead. Our approach differs conceptually, utilizing a feed forward neural network (NN) to identify under/over performance by comparing a PV plant to its neighbours, namely, other plants with similar characteristics. The concept of similarity has already been covered in other studies whose objective was to monitor residential scale PV systems.
The studies [9,10] employed neighbouring systems to determine the irradiance variations due to cloud motion and then forecasted energy production using analytical models. Golnas et al. [11] predicted the output of a PV system from a regional fleet by using data from other systems in the fleet. Tsafarakis et al. [12] developed a method for fault detection considering that the power produced by a PV system is linearly related to the power produced by neighbouring PV systems. The most relevant approach to use peer systems to monitor the PV power was presented by Leloux et al. [13]. They defined a novel performance indicator called Performance to Peer (P2P) which was computed by comparing the energy production of several neighbouring PV systems. Finally, Alcañiz et al. [14] extended the work performed in [13] considering more than 12,000 PV residential systems located in the Netherlands.
This study introduces a novel approach wherein each solar plant's 15 neighbours serve as the primary reference for its performance evaluation. Our definition of a neighbour plants is not strictly related to the geographical proximity but takes into account ten dimensions of similarity. The Machine Learning model developed to monitor the performance of a PV plant comes from a previous work [15] used to predict the expected power of an inverter in a PV plant.
The substantial difference is that, in this work, the model's parameters are fitted during the training phase involving data coming from neighbouring plants and not data from the plant it's monitoring. In a second phase, although specific data from the plant is used to predict its power output, it is the parameters of the model fitted in the previous phase that are employed to evaluate the performance of the plant under analysis, that means, without retraining the model. This approach facilitates a comparison between the target plant and its neighbouring counterparts.
In particular, the study for analysis and validation of the methodology was conducted in two different areas called Region 1 and Region 2. The former includes plants with and without trackers and, since one of the feature to find neighbours is the number of trackers, two different analyses for this area were done. Region 2 comprises only plants without trackers. The paper is structured with Section 2 detailing data cleaning and preparation for the neural network model, Section 3 presenting the model, Section 4 showing the results, and Section 5 offering conclusions and further considerations.
2 Data cleaning and preparation
2.1 Finding neighbours
Given a plant with specific attributes, 10 features were utilized to identify its neighbours, they encompass:
Plant location: latitude, longitude, altitude.
Plant layout: number of trackers, number of inverters, DC rated power, AC rated power.
Environmental conditions: Global Horizontal Irradiance (GHI), Air Temperature (Tair) and turbidity.
Data regarding plant location and layout were sourced from the GreenPowerMonitor system, while environmental conditions data were obtained from the Global Solar Atlas site [16]. Turbidity data were sourced from the pvlib (Python) [17], a tool that provides a set of functions and classes for simulating the performance of PV energy systems. All the data mentioned are average yearly values. The algorithm employed to identify neighbours was the Nearest Neighbours in the Scikit-learn library [18]. This method seeks a predefined number of training samples (k) closest in distance to the analyzed point. The number of samples is usually a user-defined constant. The distance can, in general, be any metric measure. The choice of distance for determining similarity between plants was the standard Euclidean distance, considering the features mentioned earlier. For a given plant, the k plants with the shortest distance represent its k neighbours. The selection of the number k of neighbours was based on the calculation of the expected power considering different values of k. Through tests ranging from k = 2 to k = 20 it was observed that the Root Mean Square Error (RMSE) of measured power and expected power notably decreased as the number of neighbours increased. A stability point was identified around k = 15 for most plants.
2.2 Cleaning data
Historical data with a 5-minute sampling period were collected by GreenPowerMonitor. In particular, for the analysis, the same time period was considered for all plants, namely: from 01/01/2020 to 31/05/2021. They, of course, are not exempt from having errors, so a necessary pre-processing procedure was implemented to enhance data reliability for the model. This procedure involved:
Removing missing data.
Discarding out-of-range data.
Eliminating night time data.
Excluding data points along the irradiance on the plane of the array (I) vs power (P) scatter plot axes1.
Addressing discrepancies between P values and the I − T area as outlined in [15] where T denotes ambient temperature.
Determining the optimal irradiance measurements for each plant following the procedure in [19].
After the whole procedure, the data underwent a re-scaling process as follows:
where X represents any feature in the model, q50(X) is the median and q25(X) and q75(X) denote the values of the first and the third quantiles of data X, respectively. This scaling step contributes to standardizing the data for improved consistency and effectiveness within the model.
2.3 Curtailment and data reconstruction
During the data preparation phase, it was observed that curtailment had been applied to several plants. Curtailment is the deliberate reduction in output below what could have been produced in order to balance energy supply and demand or due to transmission constraints. However, for accurate data analysis, understanding the actual power production rather than the output limited by the curtailment is crucial. Due to lack of information, determining the exact power production for some plants posed challenges. To address this, a function was developed to identify intervals of curtailed power. For these points, a quadratic regression was employed to predict the power output [20]:
Finally, for those points for which the power reconstructed is higher than the power measured, the signal was reconstructed by replacing curtailed power points with those predicted by the previous regression. An illustrative example is provided in Figure 1. The figure is zoomed in on three days, depicting a power time series (blue points) with periods of reduced power to a specified maximum value. The reconstructed power points (light blue) resulted from the described procedure for identifying curtailed points (green crosses) using the developed function.
 |
Fig. 1 An example of power curtailment for a PV plant and its subsequent reconstruction. The blue lines represent the data collected by the system, representing the power plant's actual output. The green crosses mark the points identified for reconstruction based on the developed function, and the light blue lines represent the power points predicted by the quadratic regression. The light blue lines illustrate the anticipated power output without curtailment, providing insight into the plant's potential output when not subject to deliberate reduction. |
3 The model
The objective of the model is to evaluate the performance of a solar power plant. This section outlines the construction and operation of the neural network model employed for this purpose. The model is constructed using a feed forward neural network, as depicted in Figure 2. It comprises three primary components: an input layer, which receives four features and feeds them into the model; two hidden layers in between the input and output layers, each consisting of eight neurons. These hidden layers undertake various computations on the input features received from the input layer, and then transmit the processed results to the output layer. The output layer generates the final predicted values based on the received inputs.
Generally, a neural network operates through two phases: training and testing. The dataset is divided into two parts, with a larger portion employed for training and the remainder for testing. During the training phase, the model learns from the input features, and the model parameters are fitted accordingly. An optimization algorithm is used to update these parameters, while they remain unchanged in the testing phase to predict the expected output.
The novelty of this study consists in the concept that for each plant under analysis, its 15 neighbouring plants represent the most suitable reference for its performance. The evaluation process of the plant under study can be perceived by the reader as divided into two blocks. The first one includes the training and testing phases, where data pertaining to the 15 neighbouring plants are utilized as input rather than those of the plant under analysis. During the training phase, the model learns from a set of input data (70% of the total) associated with the neighbouring plants (denoted by the suffix “ng”):
Irradiance on the plane of the array (Ing),
Ambient Temperature (Tng),
Solar elevation angle (αng),
Azimuth angle (Ang).
The neighbouring training sample is employed to fit the model parameters (weights (wng) and biases (bng)), minimizing the Mean Squared Error via the ADAM optimization algorithm. This algorithm updates the model's parameters based on how well the predictions match the actual data, across all input data in batches. Subsequently, the model is tested using the remaining 30% of data, and the anticipated power output (Png) is predicted.
Once all the steps are completed, the second block starts operating. Here, the model whose parameters were fitted in the first stage, namely through data belonging to the neighbouring systems, is evaluated on the plant under analysis. This evaluation involves utilizing input data now specific to the plant it is monitoring (denoted by the suffix “pv”):
Irradiance on the plan of the array (Ipv),
Ambient Temperature (Tpv),
Solar elevation angle (αpv),
Azimuth angle (Apv).
The anticipated power output of the plant (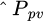 ) is then predicted. Subsequently, the model's predicted values are rescaled to their original units using the inverse formula of equation (1) and compared with the measured values (Ppv).
) is then predicted. Subsequently, the model's predicted values are rescaled to their original units using the inverse formula of equation (1) and compared with the measured values (Ppv).
To sum up, in the second block, the model is not retrained using inputs from the monitored plant; instead, the model trained in the first block, where parameters were fitted based on inputs from neighbouring plants, is utilized. In this sense, the comparison between a PV plant and its neighbours occurs. Figure 3 offers a visual representation of the operational process of the proposed neural network model. Notably, the PyTorch framework [21] is utilized, initializing weights through Xavier initialization [22]. The hyperbolic tangent (tanh) serves as the activation function, aiding neurons in producing appropriate outputs based on their inputs. The number of neurons and other model settings (refer to Tab. 1) are determined based on tests conducted in [15].
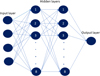 |
Fig. 2 Neural network. |
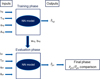 |
Fig. 3 The operation of the neural network. The subscript n on the variables refers to the neighbours, the pv one on the plant under analysis. |
Algorithm parameters.
3.1 Error measurements
Two error metrics are used to evaluate the performance of the NN model when predicting photovoltaic power: the Root Mean Square Error (RMSE) and the Mean Bias Error (MBE), both normalized to the maximum power value. They are defined using the following equations:
Here, Yi represents the values of the measured power and 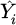 is the corresponding estimated power value, Ymax denotes the maximum value within the measured power dataset and N stands for the total number of data points.
is the corresponding estimated power value, Ymax denotes the maximum value within the measured power dataset and N stands for the total number of data points.
The MBE function as a metric capturing the overall bias of a given variable, offering insight into the systematic errors present. On the other hand, the RMSE provides a measure of individual discrepancies between predicted and actual values within an extensive set of estimations. It is noteworthy that both metrics undergo normalization, a procedural step contributing to the assessment of relative performance across disparate magnitudes. In the context of power generation, this normalization proves particularly advantageous, given the need to compare output errors from systems with divergent nominal capacities.
4 Results
The Performance Ratio (PR), as defined in [23], quantifies the efficiency of a photovoltaic system by assessing the useful energy output (measured power) relative to the energy that would be generated under continuous operation at its nominal standard conditions (STC). These conditions include a temperature of 25 °C, irradiance of 1000 W/m2, and air mass of 1.5.
To facilitate a comparative analysis between the PR of the PV plant under consideration and its neighbouring counterparts, the calculated PR is determined by dividing the measured power of the PV plant by the power predicted by the model, where inputs come from neighbours. Figures 4–6 illustrate examples of a regularly performing plant (PVregular), an overperforming plant (PVover), and an underperforming plant (PVunder), respectively. Notably, the figures are selectively zoomed in on a specific day, offering a detailed view of the observed data.
The remarkably low values observed for the error metrics, as presented in Table 2, emerge post the training phase. During this phase, the model underwent training with inputs originating from the 15 neighbours, which results in the processing of a substantial volume of data. Such a small value of the MBE indicates that the model matches the training dataset very closely and consequently, this alignment enables a meaningful comparison between the performance of the analyzed PV plant and that of its neighbouring systems (refer to [15] for further discussion of model's validation).
The concept behind the comparison between PV plants, in fact, highlights an interesting logical aspect: the performance of the plants in question must exhibit a balanced interplay. In a hypothetical scenario involving only two plants (PVA and PVB), an over performing status in PVA implies a corresponding under performing status in PVB, resulting in an approximate mean PR ∼ 1. Expanding this concept to a more complex scenario, consider PVA and its 15 neighbours forming a system of 16 PV plants. The analysis involves computing the performance ratio PRA for PVA through its 15 neighbours. Subsequently, the same process is applied to neighbour 1 through PVA and the other 14 neighbours and so forth until neighbour 15, yielding performance ratios PR1 through PR15. Does the mean value of all 16 performance ratios converge to 1? Extending this line of reasoning to encompass an entire dataset of plants, the overarching question becomes: what is the mean of the performance ratios, and do they exhibit a balancing effect? These questions are addressed in the ensuing analysis, which encompasses three datasets of plants situated in two distinct regions:
Plants with trackers in Region 1.
Plants without trackers in Region 1.
Plants with trackers in Region 2.
In the next subsections we show all detailed results for the three different cases studied.
 |
Fig. 4 An example of a PV plant regular performing. The measured power output is represented by the blue data points, while the light blue points denote the power values predicted by the model. This visual representation serves to illustrate the congruence between the actual measured power and the predicted values, affirming the regular and reliable performance of the PV plant within the context of its neighbouring systems. |
 |
Fig. 5 An example of a PV plant overperforming. The measured power output is represented by the blue data points, while the light blue points denote the power values predicted by the model. In this depiction, the observed measured power consistently surpasses the corresponding predicted values. This discrepancy between the actual and predicted power output underscores the over performance of the PV plant relative to the expectations derived from the model and its neighbouring systems. |
 |
Fig. 6 An example of a PV plant underperforming. The measured power output is represented by the blue data points, while the light blue points denote the power values predicted by the model. In this scenario, the observed measured power consistently falls short of the corresponding predicted values. This persistent disparity between the actual and predicted power output accentuates the under performance of the PV plant relative to the expectations derived from the model and its neighbouring systems. |
RMSE and MBE for regular, over performing and under performing plants respectively.
4.1 Case A
The first study was regarding 57 plants with trackers in Region 1. The visual representation as illustrated in Figure 7 depicts the physical coordinates of the plants. They have been manipulated to protect their original location. Each plant is denoted by a dot, and lines connect each plant with its respective neighbours. The use of distinct colors serves to distinguish and articulate the various connections within the dataset. This graphical depiction allows for a clear visualization of the network of relationships among the plants in this specific category, emphasizing the interconnectivity and interdependence within the dataset.
To enhance clarity and prevent confusion between lines and colors, a specific plant has been singled out for emphasis. Its connections with the 15 neighbouring plants are distinctly highlighted by more pronounced blue lines, providing a focal point for detailed examination within the broader network context.
The numerical results obtained from training and testing the model are summarized in Table 3. This table includes the PR of a randomly selected plant, the mean PR of the plant and its neighbours, and the mean PR of all plants in the dataset. These results are organized and presented for various time intervals, including days, weeks, and months. This segmentation allows for a comprehensive analysis of the performance metrics at different temporal scales. The separation into three blocks facilitates a focused examination of the PR values for individual plants, their local neighbourhoods, and the dataset as a whole, contributing to a comprehensive evaluation of the tracked performance metrics. These values align with the previous reasoning, confirming a balance in plant performances and thereby validating the model's efficacy.
An alternative visualization is presented in Figure 8, which depicts a 2D histogram plot of predicted power versus actual power for both an individual plant and each of its 15 neighbours. The changing slope in each plot reflects variations in performance, with some plants overperforming and others underperforming. Figure 9 further illustrates the distribution of performance ratios for all plants equipped with trackers in Region 1. This representation offers a comprehensive view of the performance characteristics within this subset of the dataset.
 |
Fig. 7 Plants with trackers in Region 1. Dot points represent the plants and the lines connect each plant with its neighbours. Different colors represent the different connections. As an example one of the plants and its 15 neighbours have been highlighted in dark blue. |
Numerical results related to all plants with trackers in Region 1. Results are separated in three blocks. At the top, the PR of one single plant. In the middle, the mean of the PR of one plant and its neighbours. At the bottom, the mean of the PR of all plants. These results are sampled in days, weeks, and months.
 |
Fig. 8 2D histogram of predicted power vs power for a plant and all its neighbours. The black line is the identity line. |
 |
Fig. 9 The performance ratios distribution of all plants with trackers in Region 1. |
4.2 Case B
The second study involved an examination of 65 plants without trackers in Region 1. Unlike the first case, we refrain from presenting a visual representation detailing the connections between each plant and its neighbours. This decision is rooted in the necessity to safeguard the privacy and security of the data employed in the project. Given the need to anonymize the properties and characteristics of the plants, a graphical plot revealing these connections would compromise the confidentiality of the dataset.
Numerical results for this case are summarized in Table 4, presenting only the mean PR across all plants in the dataset. Once again, the outcomes underscore a harmonious balance in plant performances, as evidenced by the mean PR hovering around 1. Figure 10 complements this insight by offering a visual representation of the distribution of performance ratios for all plants without trackers in Region 1. This illustration provides a comprehensive overview of the performance characteristics within this specific subset of the dataset, facilitating an understanding of the variability and trends in plant performances.
Numerical results related to all plants without trackers in Region 1. Results of the mean of the PR of all plants are sampled in days, weeks and months.
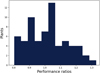 |
Fig. 10 The performance ratios distribution of all plants without trackers in Region 1. |
4.3 Case C
The third study was regarding 75 plants without trackers in Region 2. Figure 11 illustrates the connection of each plant with its neighbours. As in Figure 7, it represents the physical coordinates of the plants. Again, a specific plant has been singled out for emphasis. Its connections with the 15 neighbouring plants are distinctly highlighted by more pronounced blue lines, offering a focal point for detailed examination within the broader network context.
Numerical results are presented in Table 5, showcasing the mean PR across all plants in the dataset. Once again, the outcomes affirm a balance in plant performances, with the mean PR hovering around 1. However, upon inspecting Figure 12, depicting the distribution of performance ratios for all plants without trackers in Region 2, a notable observation emerges. Specifically, one plant exhibits a considerably higher performance ratio compared to others. The rationale behind this discrepancy lies in the fact that the neighbours of this particular plant are all deemed “underperforming,” thus elevating the plant's PR significantly in comparison.
 |
Fig. 11 Plants without trackers in Region 2. Dot points represent the plants and the lines connect each plant with its neighbours. Different colours represent the different connections. |
Numerical results related to all plants without trackers in Region 2. Results of the mean of the PR of all plants are sampled in days, weeks and months.
 |
Fig. 12 The performance ratios distribution of all plants without trackers in Region 2. |
5 Conclusions
In this study, a machine learning model was developed to monitor and compare the performance of PV plants. The model, based on a feed forward neural network, identifies under/over performance by comparing the power output of a PV plant with its neighbours, namely plants having similar characteristics. The novelties presented in this paper concern both the concept of similarity from which the neighbours of a given plant arise and the way in which the model is trained and then evaluated. In fact, it is useful to point out that the neighbours found for each plant that is being monitored are not only geographically close, but have similar characteristics that also depend on the environmental conditions and the structure of the plants.
This idea represents a novelty in the literature in the field of solar energy and further insights could prove to be very interesting to explore the concept of similarity in this scenario. In addition, the comparison between the plant under analysis and its 15 neighbours arises from the structure of the built model. In a first phase, the neural network is trained starting from inputs including historical data such as irradiance, ambient temperature, and sun's position that come from the neighbours and in a second phase it is evaluated considering the same inputs now coming from the plant itself. This is where our contribution differ from previous works.
The model was tested and validated on several plants, considering different cases: plants with trackers in Region 1, plants without trackers in Region 1, and plants without trackers in Region 2. The results demonstrate the effectiveness of the model in providing a balanced assessment of plant performance. The developed machine learning model, validated across different scenarios, proves to be a valuable tool for monitoring and comparing the performance of PV plants. The balanced interplay of performance ratios observed across various cases underscores the model's reliability in assessing and identifying under/overperforming plants. The model is intended to be integrated into the GreenPowerMonitor platform. This holds promise for providing a validated and practical tool for stakeholders in the solar energy sector.
Funding
This research received no external funding.
Conflicts of interest
The authors declare there is no conflict of interest related to this work.
Data availability statement
Data associated with this article cannot be disclosed due to legal reason.
Author contribution statement
All the authors were involved in the preparation of the manuscript. All the authors have read and approved the final manuscript.
References
- DNV, Energy transition outlook (2023). Available at: https://www.dnv.com/energy-transition-outlook/download-thank-you.html [Google Scholar]
- A. Alcañiz, D. Grzebyk, H. Ziar, O. Isabella, Trends and gaps in photovoltaic power forecasting with machine learning, Energy Rep. 9, 447 (2023) [Google Scholar]
- L. Li, S. Wen, M. Tseng, C. Wang, Renewable energy prediction: a novel short-term prediction model of photovoltaic output power, J. Clean. Prod. 228, 359 (2019) [Google Scholar]
- M. Trigo-González, F.J. Batlles, J. Alonso-Montesinos, P. Ferrada, J. del Sagrado, M. Martínez-Durbán, M. Cortés, C. Portillo, A. Marzo, Hourly PV production estimation by means of an exportable multiple linear regression model, Renew. Energy 135, 303 (2019) [Google Scholar]
- A. Mellit, S. Sağlam, S.A. Kalogirou, Artificial neural network-based model for estimating the produced power of a photovoltaic module, Renew. Energy 60, 71 (2013) [CrossRef] [Google Scholar]
- G. Graditi, S. Ferlito, G. Adinolfi, Comparison of photovoltaic plant power production prediction methods using a large measured dataset, Renew. Energy 90, 513 (2016) [CrossRef] [Google Scholar]
- S. Leva, A. Dolara, F. Grimaccia, M. Mussetta, E. Ogliari, Analysis and validation of 24 hours ahead neural network forecasting of photovoltaic output power, Math. Comput. Simul. 131, 88 (2017) [CrossRef] [Google Scholar]
- L. Liu, D. Liu, Q. Sun, H. Li, R. Wennersten, Forecasting power output of photovoltaic system using a BP network method, Energy Procedia. 142, 700 (2017) [Google Scholar]
- B. Elsinga, W. van Sark, Spatial power fluctuation correlations in urban rooftop photovoltaic systems, Prog. Photovolt.: Res. Appl. 23, 1390 (2015) [CrossRef] [Google Scholar]
- V.P.A. Lonij, A.E. Brooks, A.D. Cronin, M. Leuthold, K. Koch, Intra-hour forecasts of solar power production using measurements from a network of irradiance sensors, Sol. Energy 97, 58 (2013) [Google Scholar]
- A. Golnas, J. Bryan, R. Wimbrow, C. Hansen, S. Voss, Performance assessment without pyranometers: Predicting energy output based on historical correlation, in IEEE Photovoltaic Specialists Conference (2011), pp. 1160–1172 [Google Scholar]
- O. Tsafarakis, K. Sinapis, W.G. Van Sark, PV system performance evaluation by clustering production data to normal and non-normal operation, Energies 11, 0423 (2018) [Google Scholar]
- J. Leloux, L. Narvarte, A. Desportes, D. Trebosc, Performance to peers (P2P): a benchmark approach to fault detections applied to photovoltaic system fleets, Sol. Energy 202, 522 (2020) [CrossRef] [Google Scholar]
- A. Alcañiz, M.M. Nikam, Y. Snow, O. Isabella, H. Ziar, Photovoltaic system monitoring and fault detection using peer systems, Prog. Photovolt.: Res. Appl. 30, 1072 (2022) [Google Scholar]
- G. Guerra, P. Mercade Ruiz, L. Landberg, A data-driven model for solar inverters, in 37th EU PVSEC (2020), available at https://userarea.eupvsec.org/proceedings/EU-PVSEC-2020/5DO.4.1/ [Google Scholar]
- Available at https://globalsolaratlas.info/map [Google Scholar]
- W.F. Holmgren, C.W. Hansen, M.A. Mikofski, pvlib python: a python package for modeling solar energy systems, J. Open Source Softw. 3, 29 (2018) [Google Scholar]
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot, E. Duchesnay, Scikit-learn: machine learning in Python, J. Mach. Learn. Res. 12, 2825 (2011) [Google Scholar]
- G. Guerra, P. Mercade Ruiz, G. Anamiati, L. Landberg, A study of the impact of multiple irradiance measurements on the performance of data-driven models, in 8th World conference on photovoltaic energy conversion (2022), available at https://userarea.eupvsec.org/proceedings/WCPEC-8/4BV.4.13/ [Google Scholar]
- S. Moslehi, T. Agami Reddy, S. Katipamula, Evaluation of data-driven models for predicting solar photovoltaics power output, Energy 142, 1057 (2018) [CrossRef] [Google Scholar]
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Kopf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai, S. Chintala, PyTorch: an imperative style, high-performance deep learning library, Adv. Neural Inf. Process. Syst. 32, 8026 (2019) [Google Scholar]
- X. Glorot, Y. Bengio, Understanding the difficulty of training deep feedforward neural networks, Aistats 9, 249 (2010) [Google Scholar]
- A.M. Khalid, I. Mitra, W. Warmuth, V. Schacht, Performance ratio − crucial parameter for grid connected PV plants, Renew. Sustain. Energy Rev. 65, 1139 (2016) [CrossRef] [Google Scholar]
Cite this article as: Gaetana Anamiati, Lars Landberg, Gerardo Guerra, Pau Mercadé Ruiz, Benchmarking photovoltaic plant performance: a machine learning model using multi-dimensional neighbouring plants, EPJ Photovoltaics 15, 27 (2024)
All Tables
RMSE and MBE for regular, over performing and under performing plants respectively.
Numerical results related to all plants with trackers in Region 1. Results are separated in three blocks. At the top, the PR of one single plant. In the middle, the mean of the PR of one plant and its neighbours. At the bottom, the mean of the PR of all plants. These results are sampled in days, weeks, and months.
Numerical results related to all plants without trackers in Region 1. Results of the mean of the PR of all plants are sampled in days, weeks and months.
Numerical results related to all plants without trackers in Region 2. Results of the mean of the PR of all plants are sampled in days, weeks and months.
All Figures
 |
Fig. 1 An example of power curtailment for a PV plant and its subsequent reconstruction. The blue lines represent the data collected by the system, representing the power plant's actual output. The green crosses mark the points identified for reconstruction based on the developed function, and the light blue lines represent the power points predicted by the quadratic regression. The light blue lines illustrate the anticipated power output without curtailment, providing insight into the plant's potential output when not subject to deliberate reduction. |
| In the text | |
 |
Fig. 2 Neural network. |
| In the text | |
 |
Fig. 3 The operation of the neural network. The subscript n on the variables refers to the neighbours, the pv one on the plant under analysis. |
| In the text | |
 |
Fig. 4 An example of a PV plant regular performing. The measured power output is represented by the blue data points, while the light blue points denote the power values predicted by the model. This visual representation serves to illustrate the congruence between the actual measured power and the predicted values, affirming the regular and reliable performance of the PV plant within the context of its neighbouring systems. |
| In the text | |
 |
Fig. 5 An example of a PV plant overperforming. The measured power output is represented by the blue data points, while the light blue points denote the power values predicted by the model. In this depiction, the observed measured power consistently surpasses the corresponding predicted values. This discrepancy between the actual and predicted power output underscores the over performance of the PV plant relative to the expectations derived from the model and its neighbouring systems. |
| In the text | |
 |
Fig. 6 An example of a PV plant underperforming. The measured power output is represented by the blue data points, while the light blue points denote the power values predicted by the model. In this scenario, the observed measured power consistently falls short of the corresponding predicted values. This persistent disparity between the actual and predicted power output accentuates the under performance of the PV plant relative to the expectations derived from the model and its neighbouring systems. |
| In the text | |
 |
Fig. 7 Plants with trackers in Region 1. Dot points represent the plants and the lines connect each plant with its neighbours. Different colors represent the different connections. As an example one of the plants and its 15 neighbours have been highlighted in dark blue. |
| In the text | |
 |
Fig. 8 2D histogram of predicted power vs power for a plant and all its neighbours. The black line is the identity line. |
| In the text | |
 |
Fig. 9 The performance ratios distribution of all plants with trackers in Region 1. |
| In the text | |
 |
Fig. 10 The performance ratios distribution of all plants without trackers in Region 1. |
| In the text | |
 |
Fig. 11 Plants without trackers in Region 2. Dot points represent the plants and the lines connect each plant with its neighbours. Different colours represent the different connections. |
| In the text | |
 |
Fig. 12 The performance ratios distribution of all plants without trackers in Region 2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.