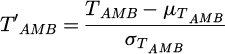EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 14 (2023) EPJ Photovolt., 14 (2023) 30 Full HTML
Issue
EPJ Photovolt.
Volume 14, 2023
Special Issue on ‘EU PVSEC 2023: State of the Art and Developments in Photovoltaics’, edited by Robert Kenny and João Serra
Article Number 30
Number of page(s) 10
Section Modelling
DOI https://doi.org/10.1051/epjpv/2023018
Published online 23 October 2023

© G. Guerra et al., Published by EDP Sciences, 2023

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

Solar photovoltaic (PV) energy has seen a remarkable growth over the last 2 decades; constant technology improvements and cost reductions have allowed yearly installations to rise from 1 GW in 2004, 10 GW in 2010 to 150 GW installed in 2021, despite the continuous supply-chain disruptions caused by the pandemic and other geo-political events. It is expected that total installed capacity will reach 14.5 TW by 2050, which represents a 24-fold increment with respect to 2020; furthermore, solar PV will experience a reduction of the Levelised Cost of Energy (LCOE) from around 50 USD/MWh in 2022 to around 30 USD/MWh by mid-century [1].

Solar PV will not only grow in capacity but will also increase its contribution to electricity generation; grid-connected solar PV electricity will grow from 3.2% of global grid electricity generation in 2019 to 30% by 2050, reaching 52 and 50% of the total generation in the Indian subcontinent and Middle East and North Africa, respectively. The increment in electricity generation will be supported by the rise of PV + storage facilities, which will amount to 5 TW of installed capacity (included in the total 14.5 TW) [1].

The significant role of future solar PV means that it is crucial to guarantee a reliable and profitable long-term operation, especially related to its ability to continue generating electricity according to the manufacturer's specifications. The power production of PV modules can be affected by multiple degradation mechanisms throughout its operational lifetime. Among the most common are hot spots, corrosion, discoloration, delamination, cracks, potential-induced degradation, light-induced degradation, bubbles, etc [2]. Although these mechanisms will not result in a complete failure, they will reduce the modules' capability to produce energy, jeopardizing the overall technical and financial performance of a PV plant. Furthermore, degradation can also occur at system level due to mismatch in performance and degradation rates among modules, as well as aging in other components such as inverters, cables, etc.

The long-term degradation of PV modules and systems has been widely investigated with many studies focusing on the performance of specific PV module technologies and the influence of climate conditions on them [3–9]. At system level, median degradation rates of 0.5–0.7% per annum are reported in the literature [10–15]. Calculation of degradation rates has also been widely studied, multiple methodologies with different approaches for calculating degradation rates have been proposed [16–21]; [16] and [17] present a detailed review of these methods. However, most of these methodologies assume a specific degradation behaviour, typically linear or exponential [22], and require detailed metadata to define the analytical models used to determine the ideal energy production of the PV plant. Field data have demonstrated that assuming a linear behaviour may not be realistic, primarily due to the presence of initial degradation and subsequent wear-out effects [9]. These aspects represent serious limitations when modelling non-linear behaviour or when metadata is either not available or reliable, a common theme in the operation of real-life PV plants.

This paper presents a methodology for the calculation of long-term degradation of a PV plant based on neural networks (NNs). Long-term degradation is defined as the irreversible reduction in the power output at system level not only due to PV modules but other components at the PV plant. The goal of the NN is to model the PV plant's power production (PAC) as a function of irradiance on the plane of the array (IPOA), ambient temperature (TAMB), and time elapsed since the plant started operating in years (TOPE). After the NN has been trained, it is fed with mean values for IPOA and TAMB, while varying the TOPE from zero to the time corresponding to the last time stamp in the data set. The degradation rate is calculated as the derivative of PAC with respect to TOPE as it represents the rate of change of the power production with respect to time. A big advantage of this method with respect to others is that it is completely data-driven, requires no additional information, and makes no assumptions related to degradation behaviour.

The next Sections of this paper are structured as follows: Section 2 details the methodology developed to train a neural network that can be used to estimate the long-term degradation of a PV plant. Section 3 presents different case studies that show the results from the methodology and compare them to those obtained with rdtools [23], while Section 4 introduces a discussion about the methodology and the results. Finally, Section 5 summarizes the work presented in the paper with conclusions and future work.

2 Methodology

2.1 Data requirements

Conceived as a completely data-driven methodology, NN training requires only operational data signals related to IPOA, TAMB, PAC, and timestamps for the collected data points; no other specific information related to the plant's location, technology or size is needed. TOPE is calculated from the signal's timestamps using equation (1). Please note that in order to fully capture the plant's time-dependency, data signals must not present important gaps in the time series. Moreover, data should be relatively free of errors; although, a data cleaning procedure has been implemented (see Sect. 2.2), forced removal of a significant amount of data points can have a negative effect on the NN's modelling capabilities.

(1)

where UTSt is the Unix timestamp at time t and UTSinit is the first recorded Unix timestamp.

2.2 Data cleaning and scaling

On-site collected data are not free of errors; therefore, a procedure for data cleaning must be implemented. The objective of this step will be to identify those points that do not conform to the plant's statistically normal behaviour. After said points have been identified, they will be removed from the data set. The followed procedure focuses mostly on cleaning data based on PAC and IPOA; moreover, it also considers out-of-range data, missing data (e.g., nulls), and duplicated time stamps.

The main steps of the data cleaning procedure are [24]:

  1. Remove missing data.

  2. Remove duplicated time stamps.

  3. Remove out-of-range data.

  4. Clean data along the axes of the IPOA vs PAC scatter plot.

  5. Remove low-power periods.

  6. Discard erroneous power values that do not conform to the relationship between IPOA, TAMB and PAC.

  7. Remove points with an IPOA value lower than 500 W / m2.

An IPOA limit of 500 W/ m2 has been set to avoid the higher uncertainty of low power values. This filter will inevitably result in a smaller training data set, which can speed-up model training. However, having multiple years of data will help ensure that the resulting data set is still sufficient for training a reliable model. Finally, when performing a degradation analysis based on mean IPOA values, not applying this condition could result in a considerably low mean IPOA value that is not significant for the long-term performance analysis. Please note that the minimum IPOA value used in step 7 of the data cleaning procedure may have to be adjusted based on IPOA distribution of the site under study to prevent excessive data loss. Filtering 60–50% of the remaining daytime data points after steps 1–6 should provide enough data for model training, while removing lower irradiance and power values.

Finally, data signals are re-scaled to have a zero mean and unity variance:

(2)

(3)

(4)

(5)

where μ and σ represent the mean and standard deviation, respectively.

2.3 Model structure

It is a well-known outcome from using NNs that, due to the stochastic nature of their optimisation, successive model trainings on the same data sets will yield similar but slightly different results; this is a significant drawback for the estimation of long-term degradation rates since the same PV plant will produce different degradation rates every time a new model is trained. To overcome this limitation, it would be necessary to train multiple NNs and use the average output of all models as the true predicted value; unfortunately, this approach would require impractical training times for PV plants with several years of operation.

A similar but more practical approach has been implemented for this work. In it multiple NNs are initialised together as a Set of Neural Networks (SNN) but only one of them is selected and updated for every batch evaluation. This will result in an ensemble of “weakly” trained NNs for which the final prediction is calculated as the average of all NNs [25], see equation (6). The concept behind this model is that not every NN must be fully optimised, they only need to reach a quasi-optimum state, so their prediction can be used as part of the ensemble.

(6)

where ŷ is the prediction of the target variable y, x is the vector with the input features, and N is the total number of NNs in the ensemble.

The basic model structure chosen for this work is an NN with one hidden layer and 3 neurons that uses hyperbolic tangent (Tanh) as activation function, see Figure 1. The model is purposely constrained in its size to ignore short-term effects, such as seasonality or abrupt year-to-year variations, which will result in a larger Mean Square Error (MSE) compared to a NN with an optimised structured aimed at minimizing the MSE.

thumbnail Fig. 1

Model structure.

Table 1 presents the main parameters used for model training.

Table 1

Algorithm parameters.

2.4 Model training

Model training requires initialising two different sets of NNs with identical weights. The first set (SNN) is trained by minimising the MSE. For every batch evaluation one NN is chosen at random and the selected network will be the only one to evaluate the batch data and whose weights and biases will be updated by the optimisation algorithm. Although seemingly complicated, all necessary steps to prevent the propagation of gradients to the remaining NNs are handled by PyTorch [26], the chosen deep learning framework for this work.

The second set of NNs (SNNt) is updated by applying an Exponentially Weighted Moving Average (EWMA) to the weights of SNN at the end of every optimisation step, see equation (7). EWMA has been utilised in the field of Deep Reinforcement Learning to help prevent overestimation of future rewards and stabilise training [27,28]; in the context of this work, EWMA was found to help stabilise the loss function during training and improve reproducibility of results.

(7)

A sanity check is performed at the end of model training on the different NNs to guarantee a minimum level of accuracy. The Root Mean Square Error (RMSE) and Mean Absolute Error (MAE) of all NNs in SNNt are verified and only those NNs with both an RMSE and MAE below the set's third quartile are kept. A pseudo-code for the complete process is presented in Algorithm 1.

Algorithm 1Training multiple neural networks

1: Choose number of networks in SNN

2: Initialise SNN with random weights

3: Copy SNN into SNNt

4: for epoch ← in total epochs do

5: for batch ← in training data do

6: Select an NN at random from SNN

7: Update weights of NN using gradient descent

8:Update weights of NN in SNNt using EWMA

9: end for

10: end for

11: Calculate RMSE and MAE for every NN in SNNt

12: Calculate third quartile RMSE (Q75RMSE)

13: Calculate third quartile MAE (Q75MAE)

14: for NN ← in SNNt do

15: if (RMSENN > Q75RMSE)∨(MAENN > Q75MAE) then

16: Remove NN from SNNt

17: end if

18: end for

2.5 Degradation rate

After training has been completed, the remaining NNs in SNNt are used to calculate the degradation rate. Mean IPOA and TAMB values are fed to the NNs, while TOPE is varied to cover the transpired operational life of the plant to obtain values for constant weather conditions. Afterwards, the degradation rate of the PV plant is calculated as the derivative of with respect to TOPE. Although maintaining constant values of IPOA and TAMB eliminates their influence, turning into a function of TOPE, it is still a challenge to estimate the derivative due to issues such as uneven spacing between data points, possible discontinuities, choice of algorithm, etc.

For PV systems the degradation rate is a metric that quantifies the rate of change in power production over time. For any modelled physical quantity that uses time as an input, the rate of change over time can be calculated as its derivative with respect to the time input. This concept is the basis for the selection of the derivative of with respect to TOPE as a mean to estimate long-term degradation or long-term rate of change of the power production over time.

In [29] the authors demonstrated how the automatic differentiation engines that power the most popular deep learning frameworks can be used to effectively calculate the derivative of the model's output with respect to any of its inputs. This capability is leveraged by the methodology to estimate the derivative of with respect to TOPE using autograd (PyTorch's automatic differentiation engine). Thanks to this feature, it is possible to calculate the degradation rate at any point using only the input signals and the model's output.

From a practical point of view, feeding mean IPOA and TAMB values, as well as TOPE, to SNNt implies creating a vector where the positions assigned to IPOA and TAMB are equal to zero and TOPE is replaced by . Furthermore, all NNs in SNNt are evaluated to generate different values of and its derivative with respect to . The values obtained from the models are re-scaled to their original units using equations (8) and (9). For every value of TOPE, the real and its derivative are calculated as the mean of all NNs in the set. All values are normalised by the mean value of the first year of operation [23]; the final degradation rate is calculated as the mean of all normalised derivatives.

(8)

(9)

3 Case studies

3.1 Case study 1

The first case study uses data taken from [30] and the PV plant's characteristics can be found in Table 2.

Model training was performed following Algorithm 1 and Figure 2 presents some results from this procedure. Figure 2a shows the evolution of MSE as function of the number of epochs on a logarithmic scale for both SNN and SNNt. It can be seen from these curves that model training has converged, since MSE does not continue to improve; furthermore, SNNt presents a more stable behaviour and a slightly lower final value for MSE thanks to the application of EWMA.

As mentioned in Section 2.3, SNNt is comprised of multiple “weak” networks, which is why it is necessary to remove potential networks that may negatively influence the calculation of the degradation rate and its reproducibility, see Section 2.4. Figure 2b shows the RMSE and MAE values of all networks in SNNt, as well as those that were selected to be part of the final set of networks in SNNt. Different error measurements were calculated using the prediction of SNNt as an ensemble, see equation (6). In this case the model achieved an RMSE value of 20 kW, MAE of 14.5 kW and Mean Bias Error (MBE) of −0.06 kW. Moreover, Figure 2c presents a histogram of errors obtained from the evaluation of SNNt. The found error distribution is centred around zero and shows no significant skewness, which is expected from a well-trained model.

System degradation rate was calculated using rdtools and SNNt resulting in values of −0.47 and −0.48%/year, respectively. All calculations with rdtools were conducted following the code found in [30], which uses sensor-based data and the year-on-year methodology, whereas SNNt used the methodology presented Section 2.5. Figure 3a shows the normalised power values of all networks in SNNt (maximum and minimum values for every instance of TOPE are marked by the dashed line). One can note that even within SNNt there is still a high variability, which is why the ensemble approach was used in this work. Figure 3b shows the mean normalised degradation behaviour obtained from the SNNt and the linear curve resulting from rdtools, while Figure 3c depicts a histogram with the degradation rate's distribution for both algorithms. There are two important aspects related to Figures 3b and 3c. First, rdtools assumes a linear degradation, whereas the SNNt's trend is a learned behaviour during its training; on the other hand, the SNNt degradation histogram has been generated by sampling the derivatives generated by SNNt.

Table 2

Plant metadata.

thumbnail Fig. 2

Training results.
thumbnail Fig. 3

Degradation results.
thumbnail Fig. 4

Real vs predicted power.

3.2 Case study 2

Case study 2 was performed on data obtained from an internal database. The nominal DC power of the PV plant is 106.26 kW and data were recorded with a 5 min frequency. Unfortunately, no other detailed information is available; therefore, other required values for the analysis with rdtools are taken from Table 2. Keep in mind that accuracy and significance of the results obtained with rdtools may be compromised if the real metadata presents significant differences with respect to that from case study 1.

The trained model achieved an RMSE value of 4.15 kW, MAE of 3.06 kW and MBE of 0.005 kW. Figure 4 shows a 2D histogram of PAC vs 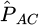, as well as a green line which represents the identity function. The 2D histogram shows that the densest regions are concentrated along the identity function. This is a sign of a model with no systematic bias and small reconstruction errors, something expected due to the low values found for the error metrics.

Degradation rates of −1.24%/year and −1.41%/year were obtained for rdtools and SNNt, respectively. Differences between degradation rates are more significant than those found in the previous Section. Although the example from where the data in Section 3.1 were taken does not provide much information about its origin, it is assumed this is a highly curated data set with accurate metadata, which would explain the negligible difference in the obtained degradation rate. On the other hand, the lack of accurate metadata for this case study would be enough to explain the differences in results; however, the most important aspect is the lack of an assumption of linear behaviour in the long-term degradation.

Figure 5a presents the normalised power that results from SNNt, the linear assumption of rdtools, a linear assumption using the mean degradation rate obtained with SNNt, and the output from training a time-independent neural network for every year of operation. As it can be seen from this Figure, degradation behaviour is not linear, and the degradation rate is not constant during the plant's operational life; see Figure 5b for the normalised degradation rates as time series. This nonlinear behaviour has been discovered thanks to the neural networks capability to model arbitrary functions.

From Figure 5 one can note that the PV plant presents positive values for the degradation rate at the beginning of its operational life; however, after reaching a maximum power value of 1.001 (i.e., zero degradation rate), the degradation rate starts to decline rapidly until reaching its minimum value of −2.74%/year. This kind of information can help to better understand the aging process of the PV plant under study.

thumbnail Fig. 5

Case study 2 − degradation results.

3.3 Other case studies and results

This Section presents results from two additional case studies that were also taken from the internal database. Just like the previous case, only the nominal DC power was available, and data were recorded with a 5 min frequency. Figures 6 and 7 show the normalised power and degradation time series, whereas Table 3 and Table 4 summarise different statistics from all case studies related to model performance and degradation rates.

Model performance, as measured by the metrics in Table 3, varies among the different case studies. The differences in these values may be due to multiple causes, such as data quality, the complexity of the time dependency, and particularities of the plant and its data collection system.

All values as a percentage of the nominal DC power.

Tables 4 and 5 provide an overview of degradation values covering all case studies. Table 4 presents additional information concerning the uncertainty associated with the proposed methodology. To this end, the mean degradation rate generated by each model within SNNt was obtained. Subsequently, the uncertainty (expressed as the standard deviation) and the range (computed as the maximum value minus the minimum value) were determined. Unlike the method in Section 2.5 where the mean degradation rate constitutes the average of all derivatives, in this analysis, the mean is independently calculated for each NN in SNNt. These values indicate that there exists a certain degree of discrepancy among the models within SNNt, as illustrated in Figure 3a. However, they also highlight the notably low uncertainty of SNNt as an ensemble. Moreover, Table 5 showcases outcomes resulting from the training of 10 distinct models, along with the subsequent mean and standard deviation. These values demonstrate that multiple evaluations of the methodology produce consistent results with a low variance.

In comparison to the proposed methodology, the sensor-based year-on-year algorithm implemented in rdtools displays notably higher levels of uncertainty, as indicated in Figure 3c and Table 4. This discrepancy is a result of the underlying assumption within rdtools that each year-on-year value contributes to the uncertainty associated with the median degradation rate, thereby introducing greater variability. On the other hand, the proposed methodology relies on the derivatives extracted from SNNt, where the uncertainty stems from the diverse behaviours exhibited by the NNs within SNNt, resulting in lower uncertainty values.

thumbnail Fig. 6

Normalised power time series − other case studies.
thumbnail Fig. 7

Normalised degradation rate time series − other case studies.
Table 3

Case studies − model performance.

Table 4

Case studies − degradation summary [%/year].

Table 5

Case studies − summary multiple models [%/year].

4 Discussion

The results obtained with the methodology introduced in this paper show how each analysed PV plant presents a distinct degradation behaviour. Although case studies 2 through 4 display some similarities, actual degradation rates, maximum normalised power and TOPE when it is reached are very different, which demonstrates the procedure can model varied complex time-dependencies. However, as proven by case study 1, the model can also model “simpler” degradation behaviours without changing its structure or training procedure. For these reasons, it is clear that the non-parametric nature of the approach and the NN's properties as universal function approximators provide an adequate framework for the analysis of arbitrary degradation characteristics.

The data-driven nature of the procedure represents a big contrast with respect to the physics-based approach used by rdtools, which relies on the plant's physical characteristics to model its power production and derive long-term degradation rates. The absence or inaccuracy of the plant's metadata will have a direct impact on rdtools' ability to generate precise results, a well-recognized limitation of physical models. Furthermore, the assumption of a linear degradation behaviour constrains the analysis by limiting the potential solution to behave in a pre-defined manner. Some of these limitations can be overcome by the use of data-driven models capable of producing robust results when little or no metadata are available; however, in spite of their adaptability and capability to model complex relationships, these models also present their own challenges. For example, low data quality or sensor degradation will affect a data-driven methodology to accurately model time-dependencies (e.g., long-term degradation) as they may become indistinguishable from the dependencies under study. Some of these drawbacks could be circumvented by introducing an independent high-quality external signal that can be used to correct any potential bias introduced by sensor degradation; however, this would also imply the need to have access to the necessary metadata to obtain a fit-for-purpose high-quality external signal.

Despite promising results, additional work is still required to assess how the selection of certain parameters will affect the results (e.g., NN size, number of trained NNs, optimisation algorithm). The general model structure and parameters were selected to provide a high reproducibility of results, while maintaining low reconstruction errors. However, other configurations may lead to lower reconstruction errors but at the price of higher variance or overfitting of certain anomalous periods of time that may affect the calculation of mean degradation rates.

Special care must be taken when analysing the derivatives provided by the model; NN training will result in a mathematically feasible set of weights, but this does not guarantee that the underlying function, and its derivatives, respects all the physical constraints of the phenomenon under study unless additional information is provided during training. Introducing additional constraints to model training may help to increase the confidence in the model's output and derivatives.

Long-term degradation is an important consideration across the PV industry. Pre-construction energy yield assessments rely on industry-accepted degradation rates and bankability of new PV projects is heavily affected by the outcome of said assessments. Therefore, it is necessary to proceed with caution when advertising new methodologies or promoting newly-found values for long-term degradation rates. The developed methodology has only been used to model the long-term degradation of individual plants; therefore, it is important to note that engineering models (e.g., linear or exponential models) may still be applicable, especially if data from multiple plants with similar characteristics are combined, potentially revealing a more distinct trend. A study that combines data from multiple PV plants would require access to important plant information, such as location, size, climate, technology, in order to ensure that only plants of similar characteristics are included and guarantee the validity of results.

5 Conclusions

Results show that the model can produce a long-term degradation trend without overfitting to shorter-term effects (e.g., seasonality) or abrupt changes in year-to-year operation, as shown by the smooth behaviour of the normalised power and degradation rate time series. Furthermore, the use of multiple NNs and EWMA help to stabilise the model's behaviour and reproducibility, whereas automatic differentiation helps automatically calculate degradation rates. Degradation rates obtained with this procedure have been compared to those using rdtools, showing various degrees of agreement between both algorithms; differences in results could be attributed to inaccuracies in the metadata used for the rdtools algorithm and the lack of an assumption of linearity.

Machine learning (ML) has been successfully applied to different problems for solar energy (e.g., irradiance forecast, condition monitoring, performance prediction [31]); furthermore, the field continues to advance at an incredible pace with new algorithms and techniques appearing frequently. This work makes use of a combination of well-known ML techniques as a way to model long-term degradation; the results also show that these techniques can also be used to understand and retrieve information from the system under study. It should be expected that researchers will continue to use ML to create innovative applications and find new solutions to the industry's problems.

Finally, future work should be aimed at evaluating a larger number of PV plants, comparing results to other algorithms, and understanding the NN's limitations to modelling arbitrary degradation trends, as well as, the real uncertainty and accuracy around the true degradation rate. Furthermore, additional effort is required to develop a model that is capable of coping with sensor degradation or systematic loss of calibration (especially IPOA) without compromising the robustness in the estimation of long-term degradation rates. Moreover, the methodology should be further enhanced with a model that it can not only model degradation but also predict its behaviour into the future; keep in mind that in its present form the model is not presented with TOPE values outside of those seen during training.

Author contribution statement

All the authors were involved in the preparation of the manuscript. All the authors have read and approved the final manuscript.

References

  1. DNV, Energy transition outlook (2022). Available at: https://www.dnv.com/energy-transition-outlook/download.html, visited on 14/09/2023 [Google Scholar]
  2. J. Kim, M. Rabelo, S.P. Padi, H. Yousuf, E.-C. Cho, J. Yi, A review of the degradation of photovoltaic modules for life expectancy, Energies 14, 4278 (2021) [CrossRef] [Google Scholar]
  3. T. Ishii, A. Masuda, Annual degradation rates of recent crystalline silicon photovoltaic modules, Progr. Photovolt.: Res. Appl. 25, 953 (2017) [CrossRef] [Google Scholar]
  4. R. Eke, H. Demircan, Performance analysis of a multi crystalline Si photovoltaic module under Mugla climatic conditions in Turkey, Energ. Conver. Manage. 65, 580 (2013) [CrossRef] [Google Scholar]
  5. V. Sharma, A. Kumar, O. Sastry, S. Chandel, Performance assessment of different solar photovoltaic technologies under similar outdoor conditions, Energy 58, 511 (2013) [CrossRef] [Google Scholar]
  6. B. Marion, M.G. Deceglie, T.J. Silverman, Analysis of measured photovoltaic module performance for Florida, Oregon, and Colorado locations, Sol. Energy 110, 736 (2014) [Google Scholar]
  7. M. Schweiger, J. Bonilla, W. Herrmann, A. Gerber, U. Rau, Performance stability of photovoltaic modules in different climates, Progr. Photovolt.: Res. Appl. 25, 968 (2017) [CrossRef] [Google Scholar]
  8. P. Rajput, G. Tiwari, O. Sastry, B. Bora, V. Sharma, Degradation of mono-crystalline photovoltaic modules after 22 yr of outdoor exposure in the composite climate of India, Sol. Energy 135, 786 (2016) [CrossRef] [Google Scholar]
  9. D.C. Jordan, T.J. Silverman, B. Sekulic, S.R. Kurtz, PV degradation curves: non-linearities and failure modes, Prog. Photovolt. Res. Appl. 25, 583 (2017) [CrossRef] [Google Scholar]
  10. D.C. Jordan, S.R. Kurtz, Photovoltaic degradation rates − an analytical review, Progr. Photovolt.: Res. Appl. 21, 12 (2013) [CrossRef] [Google Scholar]
  11. C. Deline, R. White, M. Muller, K. Anderson, K. Perry, M. Deceglie, L. Simpson, D. Jordan, PV fleet performance data initiative program and methodology, in 47th IEEE Photovoltaic Specialists Conference (PVSC), 2020, pp. 1363–1367 [CrossRef] [Google Scholar]
  12. F. Carigiet, C.J. Brabec, F.P. Baumgartner, Long-term power degradation analysis of crystalline silicon PV modules using indoor and outdoor measurement techniques, Renew. Sust. Energ. Rev. 144, 111005 (2021) [CrossRef] [Google Scholar]
  13. M. Bolinger, W. Gorman, D. Millstein, D. Dirk, System-level performance and degradation of 21 GWDC of utility-scale PV plants in the United States, J. Renew. Sust. Energ. 12, 043501 (2020) [CrossRef] [Google Scholar]
  14. K. Kiefer, B. Farnung, B. Müller, Degradation in PV power plants: theory and practice, in 35th EU PVSEC, 2018 [Google Scholar]
  15. D.C. Jordan, S.R. Kurtz, K. VanSant, J. Newmiller, Compendium of photovoltaic degradation rates, Prog. Photovolt.: Res. Appl. 24, 978 (2016) [CrossRef] [Google Scholar]
  16. A. Phinikarides, N. Kindyni, G. Makrides, G.E. Georghiou, Review of photovoltaic degradation rate methodologies, Renew. Sust. Energ. Rev. 40, 143 (2014) [CrossRef] [Google Scholar]
  17. S. Lindig, I. Kaaya, K. Weiß, D. Moser, M. Topic, Review of statistical and analytical degradation models for photovoltaic modules and systems as well as related improvements, IEEE J. Photovolt. 8, 1773 (2018) [CrossRef] [Google Scholar]
  18. M. Theristis, A. Livera, C.B. Jones, G. Makrides, G.E. Georghiou, J.S. Stein, Nonlinear photovoltaic degradation rates: modeling and comparison against conventional methods, IEEE J. Photovolt. 10, 1112 (2020) [CrossRef] [Google Scholar]
  19. I. Romero-Fiances, A. Livera, M. Theristis, G. Makrides, J.S. Stein, G. Nofuentes, J. de la Casa, G.E. Georghiou, Impact of duration and missing data on the long-term photovoltaic degradation rate estimation, Renew. Energy 181, 738 (2022) [CrossRef] [Google Scholar]
  20. IEA PVPS Task 13, Assessment of performance loss rate of PV power systems, performance, operation and reliability of photovoltaic systems (2021) [Google Scholar]
  21. D.C. Jordan, C. Deline, S.R. Kurtz, G.M. Kimball, M. Anderson, Robust PV degradation methodology and application, robust PV degradation methodology and application, IEEE J. Photovolt. 8, 525 (2018) [CrossRef] [Google Scholar]
  22. IEA PVPS Task 13, Service life estimation for photovoltaic modules, performance, operation and reliability of photovoltaic system (2021) [Google Scholar]
  23. M.G. Deceglie, A. Nag, A. Shinn, G. Kimball, D. Ruth, D. Jordan, J. Yan, K. Anderson, K. Perry, M. Mikofski, M. Muller, W. Vining, C. Deline,RdTools, version 2.0.5, Computer Software [Google Scholar]
  24. G. Guerra, P. Mercade Ruiz, L. Landberg, A data-driven model for solar inverters, in 37th EU PVSEC, 2020 [Google Scholar]
  25. D. Optiz, R. Maclin, Popular ensemble methods: an empirical study, J. Artif. Intell. Res. 11, 169 (1999) [CrossRef] [Google Scholar]
  26. A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Kopf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai, S. Chintala, PyTorch: an imperative style, high-performance deep learning library, Adv. Neural Inf. Process. Syst. 32, 8024 (2019) [Google Scholar]
  27. H. van Hasselt, A. Guez, A.D. Silver, Deep reinforcement learning with double Q-learning, in AAAI'16: Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence (ACM, 2016), pp. 2094–2100 [Google Scholar]
  28. T.P. Lillicrap, J.J. Hunt, A. Pritzel, N. Heess, T. Erez, Y. Tassa, D. Silver, D. Wierstra, Continuous control with deep reinforcement learning, arXiv:1509.02971 (2019) [Google Scholar]
  29. M. Raissi, P. Perdikaris, G.E. Karniadakis, Physics informed deep learning (Part I): data-driven solutions of nonlinear partial differential equations, arXiv:1711.10561 (2017) [Google Scholar]
  30. https://github.com/NREL/rdtools/blob/master/docs/degradation_and_soiling_example_pvdaq_4.ipynb [Google Scholar]
  31. D. Rangel-Martinez, K.D.P. Nigam, L.A. Ricardez-Sandoval, Machine learning on sustainable energy: a review and outlook on renewable energy systems, catalysis, smart grid and energy storage, Chem. Eng. Res. Des. 174, 414 (2021) [CrossRef] [Google Scholar]

Cite this article as: Gerardo Guerra, Pau Mercade-Ruiz, Gaetana Anamiati, Lars Landberg, Long-term PV system modelling and degradation using neural networks, EPJ Photovoltaics. 14, 30 (2023)

All Tables

Table 1

Algorithm parameters.

In the text
Table 2

Plant metadata.

In the text
Table 3

Case studies − model performance.

In the text
Table 4

Case studies − degradation summary [%/year].

In the text
Table 5

Case studies − summary multiple models [%/year].

In the text

All Figures

thumbnail Fig. 1

Model structure.
In the text
thumbnail Fig. 2

Training results.
In the text
thumbnail Fig. 3

Degradation results.
In the text
thumbnail Fig. 4

Real vs predicted power.
In the text
thumbnail Fig. 5

Case study 2 − degradation results.
In the text
thumbnail Fig. 6

Normalised power time series − other case studies.
In the text
thumbnail Fig. 7

Normalised degradation rate time series − other case studies.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.