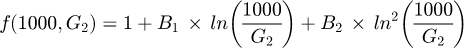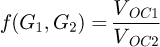| Issue |
EPJ Photovolt.
Volume 15, 2024
Special Issue on ‘EU PVSEC 2024: State of the Art and Developments in Photovoltaics’, edited by Robert Kenny and Gabriele Eder
|
|
|---|---|---|
| Article Number | 39 | |
| Number of page(s) | 10 | |
| DOI | https://doi.org/10.1051/epjpv/2024033 | |
| Published online | 19 November 2024 | |
https://doi.org/10.1051/epjpv/2024033
Original Article
Using the equivalent cell temperature for power matrix calculations
European Commission, Joint Research Centre, Ispra (VA), Italy
* e-mail: Hanna.ELLIS@ec.europa.eu
Received:
28
June
2024
Accepted:
8
October
2024
Published online: 19 November 2024
Performing measurements and compiling a power matrix (IEC 61853-1) is a useful tool for illustrating the energy production of a PV module at different levels of irradiance and temperature. At the European Solar Test Installation (ESTI) a steady-state solar simulator can be used to determine these matrices. The steady-state solar simulator irradiates the PV module from the front side, which heats the module to the desired temperature. However, this causes a temperature difference between the front surface of the module and the rear, where the temperature sensor is attached. This temperature difference, between the measured module temperature (Tm) and the temperature of the cell junction, gives rise to errors. In this paper, a correction procedure according to the determination of the equivalent cell temperature (ECT) of photovoltaic devices by the open-circuit voltage method in IEC 60904-5 is proposed and evaluated. In this study the difference between the Tm and the ECT was determined to about 1 °C to 3 °C, resulting in a deviation of the Pmax value in the power matrix up to about 1.5%, for a monocrystalline PV module.
Key words: Equivalent cell temperature / power matrix / steady-state solar simulator / IEC 60904-5 / IEC 61853-1
© H. Ellis et al., Published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
As photovoltaics (PV) is seen as one of the key technologies in the energy transition, it is of great importance that it is evaluated appropriately. A PV module can be characterized by its power matrix (PM) [1] which gives the energy production over a range of different irradiances and temperatures.
At ESTI the PM measurements can be performed using a large area steady-state solar simulator (Apollo). When measuring the PM the procedure is the following, I-V curves are measured at specific irradiances and temperatures. Initially the PV module is cooled in a climatic chamber to around 5 °C, before mounting on the steady-state solar simulator and starting the measurements. Typically, the starting temperature of the module slowly rises during the installation process and is between 10 °C and 15 °C when the first I-V curve is taken. As the module heats up under the steady-state irradiance, I-V curves are periodically measured. When comparing the PM measured using a different system (Pasan IIIc solar simulator with climatic chamber) a discrepancy was observed to the PM measured using the Apollo steady-state solar simulator. The discrepancy was greater for the VOC and Pmax values due to the greater temperature coefficients, while less pronounced for the ISC values.
The reason for the discrepancy was concluded to be the difference between the cell temperature and the measured temperature (the temperature sensor is attached to the module back sheet).
A temperature regulation for a full size PV module on the large area steady-state solar simulator is not available. This would be preferable and could be achieved by enclosing the module in a temperature controlled chamber with a glass window. However, as this is not available, in order to measure a range of module temperatures ESTI chooses to start measurements with a cold (below 15 °C) module and irradiating with the solar simulator to achieve the desired temperature. As the module heats up the I-V curves are measured resulting in a range of module temperatures. On the set-up ESTI can reach module temperatures of 75 °C using near full irradiance (1250 W/m2). For measurements at lower irradiances the module will stabilize at lower temperatures. In order to measure the I-V curves at the higher temperatures for lower irradiances, ESTI exposes the module to full irradiance and then measures the I-V curves while the module is cooling under the lower irradiance. Consequently, the PV module will be in transient temperature states rather than at thermal equilibrium when measuring. At 1000 W/m2, the full temperature range can be covered by continuously illuminating the module. However, it is unlikely that the temperature difference between cell junction and sensor will be constant during the PM measurement procedure.
In literature, a temperature drop between the PV cell and the rear surface of the module has been observed for outdoor installations [2,3]. At thermal equilibrium and with an irradiance of 1000 W/m2 crystalline silicon modules usually present a temperature drop of 2 °C to 3 °C [2,3]. When predicting performance of PV arrays, the undesired temperature offset and measurement lag observed under outdoor conditions, can be overcome by calculating the average temperature of all cells in the module by measurements of its open-circuit voltage [2].
In order to correct the PM measured by the steady-state solar simulator Apollo a correction procedure according to the Determination of the Equivalent Cell Temperature (ECT) of Photovoltaic Devices by the Open-Circuit Voltage Method in IEC 60904-5 [4] was developed and applied.
ESTI code and cell type of PV modules.
2 Material and methods
2.1 Materials
Commercially available PV modules, all with polymer back sheet and metal frame, were used in the study. A list of the PV modules used, their internal ESTI code and cell type are given in Table 1.
2.2 Methods
The method for correcting the PM using the equivalent cell temperature (ECT) involves measuring the PM and separately measuring the open-circuit voltage (VOC) based on irradiance at 25 °C and temperature at 1000 W/m2, as described in IEC 60904-5. From the VOC as a function of irradiance measurements, the parameters B1 and B2 are determined while the VOC as a function of temperature provides βrel by using standard IEC 60891 [5]. Performing calculations according to IEC 60904-5 with these independently determined parameters, the ECT, i.e., the junction temperature, is obtained for each measured I-V curve. This ECT then substitutes the measured temperature Tm in the PM measurements. Finally, all PV module parameters (VOC, ISC, Pmax etc.) are determined from the recalculated PM for obtaining a full correction.
In the following subsections, the procedure for the correction is described in more detail.
2.2.1 Equations and calculations
For the junction of a PV device there are relationships describing the connection between a state 1 (G1, V1 and T1) and a state 2 (G2, V2 and T2), where G is the irradiance, V is the voltage and T the temperature.
The Equivalent Cell Temperature (ECT) is given by:
where state 1 in this case are standard test conditions (STC) (25 °C and 1000 W/m2), βrel is the relative temperature coefficient for VOC at 1000 W/m2 in %/ °C and f(1000, G2) is described by the following relationship:
where B1 and B2 are two parameters which are obtained by a separate measurement of VOC as a function of irradiance at 25 °C. The VOC2 is obtained by the following equations:
for deriving B1 and B2 measurements of VOC at different irradiances and T1 = T2 = 25 °C were performed. Since T2–T1 = 0 equation (3) becomes:
which gives:
when the VOC has been measured at different irradiances G, B1 and B2 can be obtained by fitting a polynomial of 2nd order to the data. With B1 and B2 the ECT = T2 can be calculated with equation (1).
The complete procedure is as follows, firstly measuring the PM (1), then additional measurements for obtaining the parameters for the correction according to IEC 60904-5 (2 and 3) and finally calculating the correction:
Measure I-V curves at different temperatures between approximately 10 °C and 75 °C and irradiances of 100 W/m2, 200 W/m2, 400 W/m2, 600 W/m2, 800 W/m2, 1000 W/m2 and 1100 W/m2 with the steady-state solar simulator Apollo. Data used as input data for the PM.
Measure VOC values at irradiances in the range 100 W/m2 to 1100 W/m2 measured on a Pasan IIIb pulsed solar simulator at 25 °C to obtain the B1 and B2.
Measure VOC values at different temperatures (approximately between 20 °C to 60 °C) measured on a Pasan IIIc pulsed solar simulator with a temperature controlled chamber in order to calculate the relative temperature coefficient βrel (temperature coefficient for VOC).
By using equation (5) to obtain B1 and B2 from the measurements with the Pasan IIIb and then measurements on Pasan IIIc pulsed solar simulator for obtaining the βrel, with equations (1) and (3) the temperature for each individual I-V measurement in the PM can be corrected.
2.2.2 Power matrix measurements
At ESTI the PM is measured according to the IEC 61853-1 [1]. The Apollo solar simulator and its specifics can be found in literature [6]. In brief, both the Apollo and the Pasan IIIc are connected to an in-house data acquisition system consisting of; the PV module connected to a Kepco (Bipolar Operational Power Supply/Amplifier) through a shunt box. The temperature of the reference cell used to determine the irradiance is controlled by a Peltier controller. The signal of the reference cell is converted by a separate in-house current-to-voltage amplifier. The measured signals for voltage and current of the PV module and the voltage signal from the reference cell are logged by three Agilent 34411A 61/2 Digital Multimeters (Apollo) and a Yokogawa 750 storage Oscilloscope (Pasan IIIc) respectively. The temperature of the PV module and the reference cell is logged by an ISOTECH TTI6. The entire measurement is controlled by a LabVIEW interface, which also saves the results in a text file. For the Apollo the uncertainty of the temperature readers are ± 0.1 °C, an addition of ±1 °C is added for the deviation of the reference cell temperature from 25 °C and up to ±2 °C for deviation of the module temperature and up to ±2 °C of temperature non-uniformity in the module. This gives a total uncertainty in temperature of the Apollo solar simulator of ±3.00 °C. This equates to around k = 2 uncertainty of ±0.54% for Voc and ±1.7% for Pmax.
One of the differences, and in this study the important difference, between the two systems, the Apollo and the Pasan IIIc, is the climatic chamber. In the Pasan IIIc I-V curves at varying irradiance and temperature were acquired by the pulsed-solar simulator (pulse length 10 ms) with a test plane of 2 × 1.5 m2, class A+A+A+ [7], with two xenon lamps, coupled with the temperature controlled chamber. In the temperature chamber the circulating air is conditioned (by electrical resistance heating elements for higher temperatures and refrigeration exchangers for lower temperatures) and contained by low-iron-content glass window. The reduction in irradiance as seen by the module was taken into account. The mismatch factor (MMF) was applied by scaling to the STC value, as the reference device and the module are well matched MMF was not recalculated. The PV module temperature is kept constant for 5 min (± 0.5 °C) before taking the I-V measurement. For the Pasan IIIc the uncertainty of the temperature readers are ± 0.1 °C, an additional ±0.5 °C is added for the deviation of the reference cell temperature from 25 °C, and also ±0.5 °C deviation of the module from target and ±1 °C of temperature non-uniformity in the module. This gives a total uncertainty in temperature of the Pasan IIIc solar simulator of ±1.25 °C. This equates to around k = 2 uncertainty of ±0.22% for Voc and ±1.5% for Pmax.
2.2.3 Voltage as a function of irradiance measurements
The VOC was measured at 25 °C for irradiances in the range 100 W/m2 to 1100 W/m2 with a Pasan IIIb solar simulator system. The measurement system is identical to the one for the Pasan IIIc described above. As only the VOC is of interest, the PV module was directly connected to the Yokogawa 750 Oscilloscope, thereby simplifying the measurement set-up.
As an example, the quotas of VOC, STC and VOC2 against irradiance for the HJT module (WT75) are shown in Figure 1. From this B1 and B2 are obtained as 0.0292 and 0.0051 respectively.
 |
Fig. 1 Measured open-circuit voltage values against logarithm of irradiances for a HJT PV module (WT75), which gives the B1 and B2 values. |
2.2.4 Voltage as a function of temperature
The VOC was measured at 1000 W/m2 as a function of temperature in a Pasan IIIc solar simulator system as described above. As only the VOC is of interest, the PV module was directly connected to the Yokogawa 750 Oscilloscope, thereby simplifying the measurement set-up.
As an example, the determination of the temperature coefficient for voltage βrel for a HJT PV module (WT75) is shown in Figure 2.
 |
Fig. 2 Measured VOC values for the HJT module (WT75) against temperature, which gives the βrel = −0.2333%/ °C. |
2.2.5 Round robin measurements
Within the EURAMET project METRO-PV, an interlaboratory comparison (round robin) between six partners for measurement of PM according to IEC 61853-1 was made. ESTI participated with its measurements from the Apollo, without any correction for ECT. Upon preliminary comparison of the results obtained, the VOC as measured by ESTI deviated significantly from those of the other participants which used pulsed solar simulators. With the latter the temperature control of the PV modules is significantly easier. Furthermore, the measured values of VOC are mainly influenced by PV module temperature, and only marginally by other factors such as irradiance. Therefore, the agreement in VOC between the participants reflect mainly the quality of temperature adjustment and control, as significant effects on VOC from other factors (e.g. deviation of irradiance from target value) can be excluded.
3 Results
The ECT can be calculated (Eq. (1)) for all I-V measurements in the PM from Apollo using the respective measured VOC and the correction coefficients B1 and B2 as well as βrel obtained from the separate measurements (see above). The difference between the measured temperatures Tm and the calculated ECT against the calculated ECT is shown for the polycrystalline module OP51 in Figure 3. Up to about 50 °C the ECT is about 2 °C higher than Tm measured on the back side of the module. This is due to the module being continuously heated by the simulated solar irradiance and the junction heating up faster than the back side of the module. For irradiances of 600 W/m2 and below, this changes above 50 °C, with the ECT mostly being lower than Tm. This is explained by the measurement strategy. As these low irradiances are not sufficient to heat the module beyond 50 °C, the irradiance is temporarily increased to heat the module to higher temperatures and then lowered again to the desired level for taking the measurement. The negative temperature difference in Figure 3. could be explained by the outer surface of the PV module cooling down slower than the actual cell temperature.
With the new temperature values (TECT) the PM measured in the Apollo solar simulator was recalculated. In Table 2, the differences in the maximum power (Pmax) for the full PM are shown for the polycrystalline module OP51.
For the temperature of 25 °C the differences are well below 0.50%, however for other temperatures and in particular the lower irradiances the differences are higher up to 2.51%, see 75 °C where the differences are 1.70 W (2.02%) and 2.10 W (1.67%). For the temperature of 15 °C, which is essentially the start of the measurements after the module has been cooled in a climatic chamber and mounted on the simulator, the temperature state is not well defined and significant scatter in the difference between TECT and Tm is observed (see Fig. 3). For 25 °C the differences are small, although the module temperature is typically 2 °C higher than measured (Fig. 3). For typical temperature coefficients for Pmax it would be expected that the resulting differences in Pmax are well above 0.5%. This is not the case because an additional scaling is applied to the PM, adjusting Pmax at STC (25 °C and 1000 W/m2) to the calibration value of the module determined separately on the Pasan IIIb simulator. This is justified as the determination of the module calibration (i.e. at STC) on the Pasan IIIb is more accurate (lower measurement uncertainty) partly because of superior temperature control (±0.1 °C). This scaling will affect all values in the PM equally as long as the temperature difference between TECT and Tm is the same. As shown in Figure 3 this is true for all irradiances in the temperature range 20 °C to just below 50 °C, and for those the differences reported in Table 2 are small. For those measurement conditions, however, where there is a significantly different temperature gradient between cell junction and back side of the module, the differences reported in Table 2 are much higher, up to about 2 °C and 2.5%.
Due to the lack of temperature control on the Apollo, the uncertainties for the PM obtained on Apollo were first adjusted. However, in order to reduce this uncertainty, the correction procedure described here was developed.
In order to validate our correction procedure for the PM using the ECT procedure the PM which had not been corrected (Apollo before Δ (%)) and the corrected PM (Apollo ECT Δ (%)) were compared to the PM measured with the Pasan IIIc solar simulator, see Table 3. The later solar simulator is of pulsed type and has a climatic chamber, and as a consequence the temperature of the module is essentially in thermal equilibrium when the I-V measurements are taken and therefore the measured temperature represents the junction temperature. Table 2 shows that the difference to the Pasan IIIc values are consistently smaller after correction. The remaining differences are within the respective measurement uncertainties of both systems (not shown here).
The same calculations for the difference between the ECT and Tm were also performed on two other modules, HJT (W75) (Fig. 4) and monocrystalline (WT76) (Fig. 5).
As for the OP51 module, the PM measured in the Apollo solar simulator was recalculated with new temperature values (TECT). In Table 4 and 5 parts of the PM are shown for the HJT module WT75 and monocrystalline module WT76 respectively. For WT75 the differences are generally small. This is because the temperature difference (Fig. 4) is (2 ± 1) °C for the entire matrix. As discussed previously the scaling of the PM to STC will in this case work well. For WT76 on the other hand the temperature difference (Fig. 5) is different for the irradiance of 100 W/m2, leading to significant differences (Tab. 5).
 |
Fig. 3 The difference of the measured temperature (Tm) and the calculated equivalent cell temperature (TECT) as a function of equivalent cell temperature for different intensities of irradiation for a polycrystalline module (OP51). |
Difference in Pmax (W) for the PM for the polycrystalline PV module (OP51) Before and After correction of the temperature according to the ECT procedure described here. The difference, Δ in W, is the Before correction value minus the After correction value, within brackets, in percentage, the difference divided by the Before correction value.
Part of the PM, for the polycrystalline PV module (OP51) measured with Apollo where correction of the temperature according to the ECT procedure described in IEC 60904-5 has been performed (Apollo ECT Δ) and not performed (Apollo before Δ) compared to the power measured with the Pasan IIIc solar simulator. The difference Δ in W is the Pasan IIIc value minus the Apollo value, within brackets, in percentage, the difference divided by the Apollo value.
 |
Fig. 4 The difference of the measured temperature (Tm) and the calculated equivalent cell temperature (TECT) as a function of equivalent cell temperature for different irradiances for a HJT PV module (WT75). |
 |
Fig. 5 The difference of the measured temperature (Tm) and the calculated equivalent cell temperature (TECT) as a function of equivalent cell temperature for different irradiances for a monocrystalline module (WT76). |
Part of the PM, illustrating the difference in power for the heterojunction PV module (WT75) before and after correction of the temperature according to the ECT procedure described in IEC 60904−5. The difference Δ in W is the After value minus the Before value, within brackets the difference between the two values divided by the Before value giving the percentage value.
Part of the energy matrix, illustrating the difference in power for the monocrystalline PV module (WT76) before and after correction of the temperature according to the ECT procedure described in IEC 60904-5. The difference Δ in W is the After value minus the Before value, within brackets the difference between the two values divided by the Before value giving the percentage value.
3.1 Round robin verification
ESTI participated in a round robin where PMs were measured for two modules HJT (WT71) and monocrystalline (WT72). As we are interested in the effects of temperature variations and their correction, we will compare the results for the parameter VOC. This parameter was chosen as it has a significant dependence on temperature, but is only marginally affected by other deviations in the measurement set-up. On the other hand, ISC has a very low dependence on temperature but is influenced by the reference cell calibration, spatial non-uniformity and spectral mismatch. Pmax is influenced by a combination of temperature and the effects mentioned for ISC, and a simple distinction between them is impossible. Therefore, the deviation of the VOC from the average of the round robin was evaluated. Assuming that other participants were using systems with better temperature control, the average of their results might represent a suitable approximation to the best estimate of this measurand. The VOC values determined by ESTI showed a difference to that average of the other participants. Therefore, the ECT correction procedure described here was applied. However, the modules were not available any more for performing the additional measurements (to determine B1, B2 and βrel). Therefore, as an approximation, they were determined from the respective measurements in the PM. For the temperature coefficient (βrel) the measurements at 1000 W/m2 in the restricted temperature range from 20 °C to 60 °C were used. According to Figures 3–5 it can be expected that for this range the temperature difference is approximately constant (2 °C) and the temperature coefficient calculated will only be affected marginally by this difference. Similarly, B1 and B2 were determined from the VOC values in the PM at 25 °C for all irradiances. The results for the deviations of VOC Before the ECT correction and After the ECT correction, are presented in Figures 6 and 7. In both cases the results from ESTI improved becoming more consistent with the average of the other participants. The residual deviations observed in particular at 75 °C (both modules) and at 100 W/m2 (WT71) are attributed to the imperfect determination of the correction parameters. This will be tested on modules WT75 and WT76, currently ongoing, where all additional measurements were made at ESTI. However, the average results of the other participants are not yet available. When this is available further evaluation of the method will be performed. In any case the remaining discrepancies are within declared measurement uncertainties.
 |
Fig. 6 The deviation from the average results (of the round robin) for the VOC value, of ESTI Before and After ECT correction for the HJT module WT71. |
 |
Fig. 7 The deviation from the average results (of the round robin) for the VOC value, of ESTI Before and After ECT correction for the monocrystalline module WT72. |
4 Conclusion
In this paper we present a method to correct the PV module temperature measured on a steady-state solar simulator though the ECT in order to obtain more accurate measurement results, in particular for the PM according to IEC 61853-1. The PV junction temperature determined is different from the module temperature measured on the back sheet. The effect is as expected and the observed temperature differences are in accordance with expectations based on the knowledge of the measurement strategy and details. After correction the differences with measurements made on other systems with better temperature control (Pasan IIIc and within the round robin) are diminished. There are remaining differences, which, however, are covered by measurement uncertainties.
The determination of the three correction coefficients has itself an uncertainty associated to it. This is particularly true when they have to be determined from the PM itself, rather than from separate measurements. A comprehensive analysis of this effect and the sensitivity of the PM correction to variations in the correction coefficients is beyond the scope of the current paper.
At ESTI the PM measurement is scaled to match the calibration results at STC on a separate system (Pasan IIIb). This scaling mostly corrects for temperature differences, as long as the temperature difference is constant over the PM. However, in some PM measurement conditions, due to non-linear heat dissipation of PV-modules this assumption may not hold. The data presented show, that for those conditions the temperature difference is significantly different leading to higher corrections in the PM.
The current method is currently limited to PV modules based on c-Si technology, as for other PV technologies the ECT method is not necessarily applicable. However, if it can be shown that the current ECT methodology is applicable to other PV technologies (or a dedicated ECT methodology is developed) our proposed method can easily be extended to those PV technologies.
The method in this paper can be used for I-V measurements, especially on systems like steady-state solar simulators where temperature control is limited. It requires only a few additional measurements, and the correction procedure is simple. Overall, the method makes the PM measurements more accurate.
Acknowledgments
We gratefully acknowledge that the modules WT7x were made available through the project METRO-PV as well as averaged data from other participants for modules WT71 and WT72. The authors also gratefully acknowledge Tony Sample for proof-reading the manuscript and providing feedback during the writing process.
Funding
The measurements and analysis for the modules WT7x have received funding from the project 19ENG01 Metro-PV in the EMPIR programme co-financed by the Participating States and from the European Union's Horizon 2020 research and innovation programme. The research on OP51 received no external funding.
Conflicts of interest
The authors have nothing to disclose.
Data availability statement
This article has no associated data generated.
Author contribution statement
Conceptualization, E.D.D. and H.M.; Methodology, H.M.; Software, H.M.; Validation, D.P., H.E., T.L and H.M.; Formal Analysis, H.E.; Investigation, H.E.; Writing − Original Draft Preparation, H.E.; Writing − Review & Editing, H.E. and H.M.; Supervision, E.D.D.; Project Administration, E.D.D.
Disclaimer
The views expressed are purely those of the authors and may not in any circumstances be regarded as stating an official position of the European Commission.
References
- IEC 61853-1: Photovoltaic (PV) module performance testing and energy rating − Part 1: Irradiance and temperature performance measurements and power rating, 2011 [Google Scholar]
- D.L. King, PV module and array performance characterization methods for all system operating conditions, AIP Conf. Proc. 394, 347 (1997) [Google Scholar]
- S. Krauter, A. Preiss, Comparison of module temperature measurement methods, in 2009 34th IEEE Photovoltaic Specialists Conference (PVSC) (IEEE, Philadelphia, PA, USA, 2009), pp. 000333–000338, https://doi.org/10.1109/PVSC.2009.5411669 [Google Scholar]
- IEC 60904-5: Photovoltaic devices − Part 5: Determination of the equivalent cell temperature (ECT) of photovoltaic (PV) devices by the open-circuit voltage method, 2011 [Google Scholar]
- IEC 60891: Photovoltic devices − Procedures for temperature and irradiance corrections to measured I-V characteristics, 2021 [Google Scholar]
- H. Müllejans, E. Salis, D. Pavanello, G. Bardizza, J. Lopez-Garcia, W. Zaaiman, D. Shaw, T. Sample, E.D. Dunlop, Apollo large-area steady-state solar simulator as a versatile tool for PV device performance measurements, in 37th European Photovoltaic Solar Energy Conference and Exhibition (Online, 1126 (2020), p. 1126 [Google Scholar]
- IEC 60904–9: Photovoltaic devices − Part 9: Classification of solar simulator characteristics, 2020 [Google Scholar]
Cite this article as: Hanna Ellis, Harald Müllejans, Teodora Lyubenova, Diego Pavanello, Ewan D. Dunlop, Using the equivalent cell temperature for power matrix calculations, EPJ Photovoltaics. 15, 32 (2024)
All Tables
Difference in Pmax (W) for the PM for the polycrystalline PV module (OP51) Before and After correction of the temperature according to the ECT procedure described here. The difference, Δ in W, is the Before correction value minus the After correction value, within brackets, in percentage, the difference divided by the Before correction value.
Part of the PM, for the polycrystalline PV module (OP51) measured with Apollo where correction of the temperature according to the ECT procedure described in IEC 60904-5 has been performed (Apollo ECT Δ) and not performed (Apollo before Δ) compared to the power measured with the Pasan IIIc solar simulator. The difference Δ in W is the Pasan IIIc value minus the Apollo value, within brackets, in percentage, the difference divided by the Apollo value.
Part of the PM, illustrating the difference in power for the heterojunction PV module (WT75) before and after correction of the temperature according to the ECT procedure described in IEC 60904−5. The difference Δ in W is the After value minus the Before value, within brackets the difference between the two values divided by the Before value giving the percentage value.
Part of the energy matrix, illustrating the difference in power for the monocrystalline PV module (WT76) before and after correction of the temperature according to the ECT procedure described in IEC 60904-5. The difference Δ in W is the After value minus the Before value, within brackets the difference between the two values divided by the Before value giving the percentage value.
All Figures
 |
Fig. 1 Measured open-circuit voltage values against logarithm of irradiances for a HJT PV module (WT75), which gives the B1 and B2 values. |
| In the text | |
 |
Fig. 2 Measured VOC values for the HJT module (WT75) against temperature, which gives the βrel = −0.2333%/ °C. |
| In the text | |
 |
Fig. 3 The difference of the measured temperature (Tm) and the calculated equivalent cell temperature (TECT) as a function of equivalent cell temperature for different intensities of irradiation for a polycrystalline module (OP51). |
| In the text | |
 |
Fig. 4 The difference of the measured temperature (Tm) and the calculated equivalent cell temperature (TECT) as a function of equivalent cell temperature for different irradiances for a HJT PV module (WT75). |
| In the text | |
 |
Fig. 5 The difference of the measured temperature (Tm) and the calculated equivalent cell temperature (TECT) as a function of equivalent cell temperature for different irradiances for a monocrystalline module (WT76). |
| In the text | |
 |
Fig. 6 The deviation from the average results (of the round robin) for the VOC value, of ESTI Before and After ECT correction for the HJT module WT71. |
| In the text | |
 |
Fig. 7 The deviation from the average results (of the round robin) for the VOC value, of ESTI Before and After ECT correction for the monocrystalline module WT72. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.