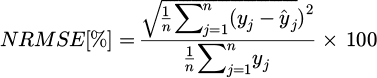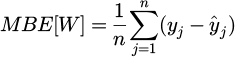| Issue |
EPJ Photovolt.
Volume 14, 2023
Special Issue on ‘WCPEC-8: State of the Art and Developments in Photovoltaics’, edited by Alessandra Scognamiglio, Robert Kenny, Shuzi Hayase and Arno Smets
|
|
|---|---|---|
| Article Number | 15 | |
| Number of page(s) | 8 | |
| Section | Deployment | |
| DOI | https://doi.org/10.1051/epjpv/2023006 | |
| Published online | 21 March 2023 | |
https://doi.org/10.1051/epjpv/2023006
Regular Article
Benchmark of eight commercial solutions for deterministic intra-day solar forecast
1
ENGIE Laborelec, Solar Lab, Rue de Rhode 125, 1630 Linkebeek, Belgium
2
ENGIE Green, 215 rue Samuel Morse, 34000 Montpellier, France
* e-mail: jonathan.lehmann@engie.com
Received:
1
July
2022
Received in final form:
10
January
2023
Accepted:
20
January
2023
Published online: 21 March 2023
Continuous increase of the production of photovoltaic energy requires precise forecasting to ensure grid stability. This paper presents a detailed benchmark of eight commercial forecasting solutions for intra-day solar forecasts. The comparison was carried out on a period of six months, from November to May 2021, on seven different PV plants located in different countries of the northern hemisphere. Performance evaluation metrics MAE, RMSE and MBE are used in order to analyze the forecasting precision. It is shown that forecasting solar power remains challenging, as shown by the important dispersion between the actors that we have observed.
Key words: Forecasting / satellite / benchmark / intra-day / forecast accuracy / solar power
© J. Lehmann et al., Published by EDP Sciences, 2023
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
In order to increase the penetration rate of solar energy into the electricity grid while ensuring the supply-demand balance, accurate forecast of photovoltaics energy is needed. Forecasts can be classified depending on the time horizon of prediction. Typically three categories are distinguished: intra-hour forecasts, for time horizons below 1 h, intra-day forecasts, for time horizons from 1 h to 6 h and finally inter-day forecasts for time horizon from 24 h to several days. In addition, forecasts can also be based on deterministic models, where the results are point forecasts or probabilistic models that incorporate the level of uncertainty associated with a forecasted value.
Numerous techniques exist for intra-day forecasting, Sobri et al. [1] classified the solar forecasting techniques into three major categories: time-series statistical methods that try to reconstruct the relations between historical meteorological data and power produced, physical models that use physical measurements such as satellite images as inputs and ensemble methods that combine both statistical methods with physical inputs. For time horizons in the range from 1 to 6 h, models that combine satellite images or statistical analysis with NWP (Numerical Weather Predictions) forecasts have shown good precisions [2–4]. NWP forecasts are particularly suited to forecast solar irradiation for lead times higher than 3–4 hours [2,5,6]. However, NWP forecasts often contain model-led bias. Thus, post-processing methods involving ground measurements or satellite data are needed to improve their accuracy [4,6,7]. Recently Bellinguer et al. [8] demonstrated an improvement of 40% by combining a spatio-temporal model with NWP and satellite images. An improvement of 5.68% of the Mean Average Error (MAE) was also demonstrated by Mendonça de Paiva by combining machine learning forecast algorithms with additional weather variables [9]. Other works evidenced how combining several machine learning approaches can improve the forecasting precision [2,10–12]. Among the work published, [2,13,14] presented the comparison of various models on up to 6 different locations.
In this work, we present a benchmark of deterministic PV power forecasts that includes eight different commercially available forecasting solutions for time horizons from 1 to 6 h. The benchmark was carried out on a period of 6 months, from November to May 2021, on seven different PV plants located worldwide. For each PV plant, one year of cleaned historical power production and global plane of array irradiance was provided to the forecasters. The objective of our study was to compare participants between each other. Therefore, the choice was made not to include the comparison to a persistence model.
To the author's best knowledge, no papers have yet presented an extensive benchmark of commercially available solutions for intra-day forecasts.
2 Methodology
This analysis has been carried out on seven different power plants located in four different countries (Tab. 1). Small size plant between 36 kWp and 7.6 MWp were chosen as previous work demonstrated that there is a direct link between the size of a PV plant and the power fluctuations, with bigger plants smoothing variations [15]. The selected PV plants are ground based, rooftop or even floating installations and all of them have a fixed structure. It should be noted that commercial scale PV installation have usually limited budget and thus they might experience equipment failure, limited maintenance or be poorly instrumented. As a consequence, flexible but precise forecasting tools are needed.
Under the Köppen climate classification, the PV plant are located in diverse areas, with climates varying between humid continental, characterized by a warm summer and a cold winter, and Mediterranean climate, characterized by sunny conditions with hot and dry summers and mild winters. Previous works demonstrated how weather conditions impact the forecasting precision [16].
For each PV plant, one year of cleaned historical data was provided to the participants. This data included active power, global plane of array irradiance and was given with time steps ranging from 10 to 30mn depending on the plant. In addition, forecasters were given access to real time on-site production data from the PV plants with a time step identical to the one of the historical data. The evaluation was then carried out on a six months period, from November to May 2021, corresponding to winter in the northern hemisphere. During this period, forecasters were required to provide every 30 min a forecast for the next 6 h for every PV plants. Only the forecasts delivered on time were kept for the evaluation. All actors delivered forecasts with a good punctuality (higher than 98%). Some minor delays or missing forecasts were observed but these were exceptional occurrences.
Eight highly recognized and international forecast providers were selected to participate to this benchmark. For confidentiality reasons, results are anonymous. Participants will be referred by numbers as shown in Table 2. In addition, the algorithms used by each participants remained unknown to us. However, some basic information given by the participants are reported in Table 2. It can be seen that all participants use NWP to provide their forecasts. Only three actors do not rely on satellite images. One actor mentioned that satellite images are never used to compute forecasts while two of them mentioned technical issues or geographical limitation that they faced when including satellite images to compute their forecasts. Only one actor does not use on-site irradiance nor real time on-site production. Finally, concerning on-site real time data production, several actors discarded it as time lags and quality problems were experienced during this benchmark.
To evaluate the precision of the forecast the root mean square error (RMSE), the mean absolute error (MAE), the mean bias error (MBE) and their normalized counterparts were used as metrics. MAE represents the mean difference between the predictions and the actual power measurements. Similarly, RMSE measures the mean error by calculating the square root of the average of squared differences between forecasted values and actual observations. Both metrics are negatively-oriented scores, which means lower values are better. RMSE considers square of error and thus gives higher weight to large errors. MBE is used to calculate the average bias in the forecast. It identifies the overestimation or underestimation in the results provided by the model. MBE is not a measure of the quality of the forecast by itself but can provide useful information regarding possible improvements [5,7,17]. The normalization was carried out by dividing the metric calculated over a certain period by the average power produced during the same period.
where n is the number of samples, yj the power produced at a given time j and  the power forecasted at a given time j.
the power forecasted at a given time j.
Finally, we define KPV, the clear-sky index as the ratio between the measured plane of array irradiance and the clear-sky plane of array irradiance. In this application, the Ineichen–Perez model clear-sky model has been used. This clear sky index has previously been used in multiple publications to classify days [18,19]. However, here the choice was made not to use the KPV to classify days but to use it to classify each data point. The KPV ranges from 0 to 1 with KPV < 0.4 for overcast weathers conditions, 0.4 < KPV < 0.7 for mixed conditions and KPV > 0.7 for clear sky weathers. The KPV is then filtered to exclude points where the irradiance is below 50 W/m2 and points were KPV is above 1. Figure 1 shows the KPV, the measured irradiance and the clear sky irradiance for a sunny and a cloudy day. It can be seen that on a cloudy day, changes in the KPV reflect the evolution of the irradiance. On a sunny day, we observe that, due to outliers in the measured irradiance, the KPV can sometimes be above 1, requesting thus a filtering of those values.
Characteristics of the PV plants.
Information given by the participants on their algorithms.
 |
Fig. 1 KPV (clear sky index), measured irradiance and clear sky irradiance for a mixed and a sunny day. |
3 Data cleaning
During the benchmark, several actors used real time data from PV plants to provide their forecasts. In order not to give a significant advantage to some actors compared to others, the on-site data was regularly checked and cleaned during the benchmark. Periods where the real time data update was stopped, or where the quality of the updated data was deteriorated were removed from the study. In addition, it should be considered that any period where power production was severely decreased due to presence of snow on the modules was removed. Table 3 represents, for each asset, the amount of data points that was kept after data cleaning.
We can see that, for all assets, at least 10% of data points were removed. Natick had several periods of underperformances due to a faulty inverter and an extended snowy period. Leeuwarden should be considered apart from other sites: an important under performance has been detected since the end of February. Thus, an important period, corresponding to 70% of the data, had to be discarded. It should be therefore noted that for this asset, the evaluation was carried on the months from November to February, which are the cloudiest months. Therefore, deteriorated metrics are expected. Limoges was impacted by data processing errors and almost 70 days had to be at least partially excluded. Finally, Orange was impacted by multiple inverter failure on more than 25 days. For other assets, data points were removed due to interruptions of the real time data feed or other minor technical issues.
For each asset, amount and percentage of data points that were kept, over the six months of benchmark, after cleaning of the data.
4 Results and discussion
4.1 Analysis of on-site climate
Figure 2 shows for each measurement the distribution of KPV over the seven considered PV plants during the 6 months of the benchmark. Despite the fact that the study took place during the winter period, for most of sites, we obtain a good repartition of the data points between cloudy, mixed and sunny weather conditions. Leeuwarden should be considered separately: as shown in Table 3, for this plant, 65% of the data had to be cleaned due to quality issues and the analysis was carried out on the months from November to February. As a consequence, we see that most of the data points correspond to cloudy weather conditions.
 |
Fig. 2 Clear sky index distribution for the 7 considered PV plants during the 6 months of the benchmark. |
4.2 Forecasting precision as a function of time horizon
Figure 3 represents for each site the dispersion of nRMSE for all actors and for time horizons of 1 h and 6 h. It can be seen that the precision of forecasting as well as the dispersion between the participants are both highly site dependent. For a time horizon of 1 hour, a median nRMSE of 27% is obtained for Orange, the most precisely forecasted site while a median nRMSE of 49% is calculated for Leeuwarden, the less precisely forecasted site. Concerning the dispersion between the participants it can be seen that Riom and Leeuwarden are the most dispersed sites, with, for a time horizon of 1 hour, forecasting precisions between 32% and 52% for Riom and between 45% and 58% for Leeuwarden. Conversely, Silves is the less dispersed site, with precisions between 26% and 33%.
In order to deepen the understanding of the site dependent precision, Figure 4 illustrates the nRMSE as a function of forecast horizon for all participants and for the following PV plants: Silves, Richmond, Limoges and Riom. These sites were chosen because of their representativity: Silves is with Orange the best performing site while Richmond and Limoges exhibits average dispersion and precision and finally Riom is among the sites with the most dispersion and worst precision. To allow for easier reading, only the nRMSE will be represented.
In Figure 4, as expected, we observe for Silves high precision (between 25% and 35%) and low dispersion for all actors. Concerning Richmond, Limoges and Riom, the results show a more important dispersion (from 25% to 55%). It can be seen that actor 1 is in most cases the most precise forecaster for time horizons below 3 hours while actor 6 is the most precise forecaster for time horizons above 3 hours. Finally, actors 2, 3 and 4 are the less precise forecasters.
More generally, three main behaviors can be distinguished. For some actors, such as actor 3, the precision of prediction remains constant across the whole time horizon range. Other forecasters, such as actor 7 or actor 8, deliver, for some assets, forecasts with an improved precision for small time horizons. Finally, for actors such as actor 1, we see for all assets, a better precision for short time horizons and a decrease of precision with the increase of time horizons. The constant precision for all time horizons is probably due to forecasts being only based on NWP models while the improvement of precision for short time horizons has been demonstrated to be related to the use of satellite images to compute forecasts [20,21].
Figure 5 shows for each actor nRMSE and nMAE averaged over all sites as a function of the time horizon.
Figure 5 confirms the results observed in Figure 4: for some participants, such as actor 3, the precision of prediction remains constant across the whole time horizon range while for others, such as actor 1, we see an improvement of precision for short time horizons and a decrease of precision with the increase of time horizons.
More generally, it can be seen that participant 1 is globally the best for small time horizons (<2.5 h) while actor 6 is globally the best for higher time horizons. It is interesting to note that actor 1 manages to be the best forecaster for small time horizons in spite of using only one NWP and being the only forecaster that does not use on-site irradiance nor real-time measurement. When comparing Figure 5 with Table 2, we observe that forecaster 1 and 4 benefit strongly from satellite images: their forecast quality increases significantly for small time horizons. On the other hand, forecasters 3, 5 and 6 have rather constant performances over all forecast horizons, indeed they base their forecasts only on NWP data. Their precision seems related to the number of NWP sources that are combined. It is important to highlight that including satellite images does not always guarantee a good forecasting precision. Indeed, actor 6 is among the best performers without using satellite images while actor 4 is among the less precise forecasters despite the use of satellite images.
 |
Fig. 3 Boxplot of nRMSE for all actors as a function of the PV plant for time horizon of 1 and 6 h. |
 |
Fig. 4 nRMSE as a function of forecast horizon for all participants and for Silves, Richmond, Limoges and Riom. |
 |
Fig. 5 nRMSE & nMAE as a function of forecast horizon for all participants averaged over all assets. |
4.3 Forecasting precision and bias
Table 4 sums up for a time horizon of 1 hour the nMBE and nRMSE for each actor and each site.
First, it can be seen that, for all actors biases are divided in between positive and negative values depending on the asset, indicating that no forecaster is systematically over- or under-forecasting. In addition, it can be seen that most nMBE are within +8/–8% limits except for Riom for which most forecasters, except actor 7 and 8, exbibit a strong negative bias. It is interesting to note that Riom, as shown in Figure 3, is among the sites with the most dispersion and worst precision.
When comparing actors 1 and 6, we observe that actor 6 has most of the time one of the smaller bias associated to a low dispersion. On the other hand, actor 1 exhibits an important dispersion of nMBE. Looking at Richmond or Leeuwarden, it can be seen that high nMBE seems to lead to degraded precision. Nonetheless, this does not verify with Riom.
The biases of actors 7 and 8 follow similar dynamics, with small values and low dispersion. Unfortunately, they do not manage to take advantage of their small biases to provide more accurate forecasts. Finally, actors 2, 3 and 4 show high dispersion of the bias with often some of the highest values.
nMBE & nRMSE for each actor, each site and a time horizon of 1 hour. Best results per column are in bold.
5 Conclusion
In this work, the performances of eight different commercial forecasters were compared on seven PV plants located worldwide. We have shown that intra-day forecasting is still challenging and highly depends on the PV plant characteristics and its location. For time horizons higher than 3 hours, we have demonstrated that a good integration of NWP allows a good forecast precision. On the contrary, for small time horizon, we have shown that the use of satellite images is required in order to obtain a real improvement of the forecasts' precision. Through our study, we have highlighted that the integration of satellite images remains a challenge as evidenced by the fact that several actors fail to take advantage of it to significantly improve the precision of their forecasts.
Author contribution statement
Jonathan Lehmann, Christian Koessler: have made a substantial contribution to the concept or design of the article; or the acquisition, analysis, or interpretation of data for the article; Jonathan Lehmann: drafted the article; Christian Koessler, Lina Ruiz Gomez, Stijn Scheerlinck: revised the article critically for important intellectual content and approved the version to be published.
References
- S. Sobri, S. Koohi-Kamali, N. Abd. Rahim, Energy Convers. Manag. 156, 459 (2018) [Google Scholar]
- M. David, M. Aguiar Luis, P. Lauret, Int. J. Forecast. 34, 529 (2018) [Google Scholar]
- R. Perez, S. Kivalov, J. Schlemmer, K. Hemker, Jr., D. Renne, T.E. Hoff, Sol. Energy 84, 2161 (2010) [Google Scholar]
- D. Yang, J. Renew. Sustain. Energy 11, 026101 (2019) [CrossRef] [Google Scholar]
- J. Zhang, B. Hodge, A. Florita, S. Lu, H.F. Hamann, V. Banunarayanan, in 3rd International Workshop on Integration of Solar Power into Power Systems (2013) [Google Scholar]
- P. Mathiesen, J. Kleissl, Sol. Energy 85, 967 (2011) [Google Scholar]
- D. Yang, S. Alessandrini, J. Antonanzas, F. Antonanzas-Torres, V. Badescu, H. Georg Beyer, R. Blaga, J. Boland, J.M. Bright, C.F.M. Coimbra, M. David, A. Frimane, C.A. Gueymard, T. Hong, M. J. Kay, S. Killinger, J. Kleissl, P. Lauret, E. Lorenz, D. van der Meer, M. Paulescu, R. Perez, O. Perpiñán-Lamigueiro, I. Marius Peters, G. Reikard, D. Renné, Y-M Saint-Drenan, Y. Shuai, R. Urraca, H. Verbois, F. Vignola, C. Voyant, J. Zhang, Sol. Energy 210, 20 (2020) [Google Scholar]
- K. Bellinguer, R. Girard, G. Bontron, G. Kariniotakis, in 36th European Photovoltaic Solar Energy Conference and Exhibition (2019) [Google Scholar]
- G. Mendonça de Paiva, S. Pires Pimentel, B. Pinheiro Alvarenga, E. Gonçalves Marra, M. Mussetta, S. Leva, Energies 13, 3005 (2020) [Google Scholar]
- S. Theocharides, G. Makrides, M. Theristis, G.E. Georghiou, in 36th European Photovoltaic Solar Energy Conference and Exhibition (2019) [Google Scholar]
- J. Lehmann, B. Haut, S. Scheerlinck, in 37th European Photovoltaic Solar Energy Conference and Exhibition (2020) [Google Scholar]
- P. Kumari, D. Toshniwal, J. Clean. Prod. 318, 128566 (2021) [CrossRef] [Google Scholar]
- L. Mazorra Aguiar, P. Lauret, M. David, A. Oliver, G. Montero, Energies 14, 1679 (2021) [Google Scholar]
- O. Doelle, I. Kalysh, A. Amthor, C. Ament, in International Conference on Smart Energy Systems and Technologies. (2021) [Google Scholar]
- J. Marcos, L. Marroyo, E. Lorenzo, D. Alvira, E. Izco, Prog. Photovoltaics: Res. Appl. 19, 505 (2011) [Google Scholar]
- R. Ahmed, V. Sreeram, Y. Mishra, M.D. Arif, Renew. Sustain. Energy Rev. 124, 109792 (2020) [CrossRef] [Google Scholar]
- D. Yang, W. Wang, J.M. Bright, C. Voyant, G. Notton, G. Zhang, C. Lyu, Sol. Energy 236, 743 (2022) [Google Scholar]
- M. Diagne, M. David, Ph. Lauret, J. Boland, N. Schmutz, Renew. Sustain. Energy Rev. 27, 65 (2013) [CrossRef] [Google Scholar]
- N.A. Engerer, F.P. Mills, Sol. Energy 105, 679 (2014) [Google Scholar]
- Report IEA-PVPS T16-01 (2020) [Google Scholar]
- Ph. Blanc, J. Remund, L. Vallance, in Renewable Energy Forecasting, edited by G. Kariniotakis (Woodhead Publishing, 2017) [Google Scholar]
Cite this article as: Jonathan Lehmann, Christian Koessler, Lina Ruiz Gomez, Stijn Scheerlinck, Benchmark of eight commercial solutions for deterministic intra-day solar forecast, EPJ Photovoltaics 14, 15 (2023)
All Tables
For each asset, amount and percentage of data points that were kept, over the six months of benchmark, after cleaning of the data.
nMBE & nRMSE for each actor, each site and a time horizon of 1 hour. Best results per column are in bold.
All Figures
 |
Fig. 1 KPV (clear sky index), measured irradiance and clear sky irradiance for a mixed and a sunny day. |
| In the text | |
 |
Fig. 2 Clear sky index distribution for the 7 considered PV plants during the 6 months of the benchmark. |
| In the text | |
 |
Fig. 3 Boxplot of nRMSE for all actors as a function of the PV plant for time horizon of 1 and 6 h. |
| In the text | |
 |
Fig. 4 nRMSE as a function of forecast horizon for all participants and for Silves, Richmond, Limoges and Riom. |
| In the text | |
 |
Fig. 5 nRMSE & nMAE as a function of forecast horizon for all participants averaged over all assets. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.