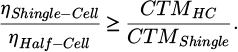EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 15 (2024) EPJ Photovolt., 15 (2024) 22 Full HTML
Issue
EPJ Photovolt.
Volume 15, 2024
Special Issue on ‘EU PVSEC 2023: State of the Art and Developments in Photovoltaics’, edited by Robert Kenny and João Serra
Article Number 22
Number of page(s) 8
DOI https://doi.org/10.1051/epjpv/2024019
Published online 11 June 2024

© J.D. Huyeng et al., Published by EDP Sciences, 2024

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

The growing demand of photovoltaic (PV) energy generation has driven the need for higher efficiency and increased power density in PV modules. To address this demand, the use of half (cut) cells [1] has emerged as a state-of-the-art technology [2], offering improved performance compared to conventional full-cell modules, due to lower generated current and therefore reduced ohmic losses. On the other hand, alternative module configurations, such as shingling, have gained attention due to their potential for further enhanced power density [3–9].

Shingling implements an overlapping of cut solar cells (typically 1/5th to 1/8th of a full cell, also referred to as shingle cell), enabling the reduction of inactive areas between cells and increasing the active cell area within a given module size [4,10]. However, the process of cutting cells for shingling introduces additional challenges in terms of cutting losses, due to unpassivated edges at the separation path [11–13]. These losses are also present in half-cut cells but are compensated by the advantages on module level and are therefore seldomly discussed. For shingle cells, the cutting-induced losses are more severe, as the edge-to-area ratio is higher.

It can be difficult to accurately access the cutting induced losses, as shingle host cells (uncut full cell with grid layout for shingle cells) have an asymmetric grid layout, which cannot be measured easily in a current-voltage (I–V) tester. Therefore, using a grid-contacting scheme is a practical method to get the I–V characteristic of shingle host cells. However, when comparing to the corresponding shingle cell or shingling module, the additional grid resistances—neglected in a grid-contacting scheme such as GridTOUCH® [14]—must be considered.

Challenges, potential advantages and optimizations of shingling have been discussed by several authors [15–17]. As shown by von Kutzleben et al. [18], (matrix) shingle modules can achieve higher efficiency than half cell modules, if (i) the same host cell performance is assumed and if (ii) the modules feature the same module area. The presented work expands on these findings, comparing half-cell and shingling modules, based on experimental results of half-cell and shingling host cells. Using Gridmaster+ [19], the same host cell and cut cell I–V characteristics are simulated as experimentally realized. The influence of grid-neglecting contacting during I–V testing is illustrated by further Gridmaster+ simulations. Moreover, the influence of cutting-induced losses on I–V characteristics is investigated by experimental results and Gridmaster+ simulations.

The experimental realization gives initial lower performance for the shingling host cells compared to half-cell host cells, due to a more conservative metallization layout and longer current paths. Using SmartCalc.Module [20] simulations it is shown that shingling modules employing edge passivation can still achieve higher efficiencies on the same module area as full or half-cell modules.

The structure of this paper is organized as follows: after this introduction, Section 2 describes the simulation framework using Gridmaster+ and SmartCalc.Module. Section 3 delves into the experimental realization of half-cell and shingle hosts, in particular their fabrication process. Section 4 presents the results and discussion, analyzing the performance of cells and modules. Finally, Section 5 provides a conclusion summarizing the main findings.

2 Simulation framework using Gridmaster+ and SmartCalc.Module

To enable further analysis of cell and module effects, the “Gridmaster” simulation framework [21] has been recently extended to the so-called “Gridmaster+” [19]. It can account for edge recombination in half and shingle cells [22], as well as different measurement setups used for host and cut cells1. With this the conceptual and practical differences between half and shingle cells can be quantitatively illustrated based on experimental data, as presented in this work.

We also adopted the “SmartCalc.Module” cell-to-module (CTM) loss calculator [23] to being able to import results of Gridmaster+ simulations and to extend the comparison of shingle and half-cut cells to module level.

Gridmaster fundamentally uses the two-diode model to simulate the I–V performance of a solar cell. The parameters of the two-diode model are given by the user or derived from a set of geometrical and electrical input parameters, e.g., number of electrode fingers, busbars, and their conductivities. Beside optimization of a grid layout based on these parameters, Gridmaster+ can also be used as a rapid simulation tool to replicate the performance of an experimental solar cell and analyze the influence of different parameters. It allows for the modeling of contacting schemes, cell interconnections, electrical loss distribution, and shading effects for example.

SmartCalc.Module starts at solar cell level and calculates the module performance by calculating different loss and gain channels, based on the bill-of-materials (BOM) and module design specified by the user. Validated by experimental results, it illustrates where optical or electrical effects occur and allows quick comparison of different design choices and components.

3 Experimental realization of half-cell and shingle hosts

In this study, the experimental realization of half-cell and shingle hosts is conducted on the same type of industrial “blue wafers” using passivated emitter and rear cell (PERC) technology and industrial equipment available at Fraunhofer ISE PV-TEC [24]. The “blue wafers” are solar cell precursors bought from industrial manufacturers, with all process steps performed before metallization, for example surface texturing, emitter diffusion and anti-reflection coating (hence the blue appearance). The finished cells can be seen in Figure 1.

The precursors were made from Czochralski-grown silicon with Ga-doping (p-type) in M6 wafer format (166 mm edge length). The dielectrics and metallization grid layouts are designed for bifacial applications.

The half-cell grid layout features nine busbars (9BB) with a continuous width of 0.1 mm and solder pads of 1 mm width. The busbar pitch distance is 16.8 mm. All electrodes are realized by flatbed screen printing on industrial “XH2” inline printers by EKRA. On the front side, 67 silver (Ag) fingers are printed per half cell, with a screen opening of 24 μm. On the rear side, 83 aluminum (Al) fingers per half cell are printed with a screen opening of 150 μm. Rear side Ag pads and front side Ag busbars are printed separately from the fingers (dual print).

The shingle layout is designed for 1/6th cuts (resulting in a length of about 27.7 mm). Each 1/6th shingle has one continuous front busbar with a width of 0.5 mm and one continuous rear busbar with a width of 1.0 mm. The 128 front side Ag fingers are printed with a screen opening of 33 μm. The 166 rear side Al fingers are printed with a 200 μm screen opening. Fingers and busbars on both sides are printed in dual print.

The wider fingers for the shingle grid are used to account for the longer current path compared to the 9BB configuration, although no optimization was done. Also, the shingle front busbar width is chosen conservatively to ensure a high tolerance for shingling interconnection. These design choices result in 2.8% higher nominal shading for the shingle host cells compared to the half-cell host cells, reducing the current output of those cells. The width of the front busbars, and therefore the photoactive area, can be reduced by a smaller shingle-to-shingle overlap in case of an industrial production with improved shingling tolerances. This can save costs by reducing the amount of Ag per cell and improve the output density.

Before the printing, laser contact opening (LCO) was performed on the rear side according to the Al finger layout by an industrial “ILS 500 X” laser tool by Innolas. All cells were dried after each printing step and Ag and Al contacts were co-fired in an industrial “RFS-250 PLUS” fast firing oven by Rehm. The cells were measured on an industrial cell tester by Jonas & Redmann, implementing the “cetisPV” I–V testing unit by h.a.l.m..

Cell cutting was performed on the same industrial “ILS 500 X” laser tool by Innolas, using the laser scribe and mechanical cleave (LSMC) [25] process for reference of highly recombinative edges. In addition, cut cell edges were also re-passivated using the passivated edge technology (PET) [3,26]. For these cells, thermal laser separation (TLS) [27] was used on a “microDICE” tool by 3D-Micromac.

Only the results of the inner, rectangular-shaped shingles are presented in this work for simplicity. This implicates that each shingle cell has the same area and two unpassivated edges after cutting.

thumbnail Fig. 1

Photographs of bifacial PERC solar host cells with half-cell (left) and shingle metallization (right) cell layout, fabricated on the same industrial precursors in M6 wafer format at Fraunhofer ISE PV-TEC Back-End laboratory. © Fraunhofer ISE.

4 Results and discussion

This section presents the results obtained from the experiments and subsequent simulations on both solar cell and module level. The experimental data is used to derive the parameters for the initial set of simulations and further simulations based on these parameters are added to discuss the different observed effects on cell level.

4.1 Host and cut solar cells

The I–V characteristics in both host and cut cell state have been analyzed. Different effects are discussed in the following, comparing the solar cell efficiency η, the fill factor FF, the open-circuit voltage VOC, and the short-circuit current ISC.

Figure 2 shows all the variations simulated by Gridmaster+ by coloured bars. The hashed bars represent a grid-neglecting contact scheme, such as GridTOUCH®. The experimental mean values and standard deviations are given by the black symbols and error bars. The different cell states are given by the label on each bar. Not all variations have been experimentally verified, but several different configurations have been matched, which demonstrates the reliability of the simulation. The remaining differences between experimental data and simulation results is <1%rel2.

The most straightforward discussion is that of the ISC. The output current of the device is directly proportional to the active area of the solar cell. Therefore, the resulting current in the cut state is 1/2 or 1/6 of the host current. This is according to the expectation and the main motivation to use cut cells, as this reduces the ohmic losses on module level.

As mentioned before, the active area for shingle host cells is reduced by 2.8%, due to the design of the front fingers and busbars. However, it should be noted that part of this shaded area is inactive in the module due to the overlap with a then active part of the upper shingle. This is different for ribbon interconnection (as for the half-cut cells), which limits the comparability on host cell level.

Comparing cut cells and host cells, a drop in the VOC  can be observed. As long as the edges are unpassivated (i.e., directly after cleaving), they lead to additional edge recombination, reducing the VOC. This additional recombination is implemented in Gridmaster+ by the empirical model of Fell et al. [22] and matches well with the performed experiments. Switching it off illustrates the ideal case of perfectly passivated edges. Comparing this idealized simulation to the experimental result of applying the passivated edge technology (PET) shows that the performance with PET is close to the ideal case (see η, FF and VOC). The experimentally determined mean value for VOC is slightly higher than expected. In principle, the processes used to passivate the edges can also affect other areas of the cell, leading to an additional improvement of VOC, not considered in the simulation. However, the difference found here is well within the expected uncertainties of experimental and simulated results.

The FF is affected by several effects. On the one hand, a systematic drop can be observed when comparing the grid-neglecting (hashed bars in Fig. 2) and grid-including results. The increase in series resistance, considering the additional current flow in the longer grid fingers, reduces the output at maximum power point (MPP) and therefore FF. On the other hand, the unpassivated edges also affect the MPP. It is important to take this into account when comparing the host vs. the cut cell state. In the experimental results, the cut cells have been measured with grid-including contacting, while the hosts have been measured with grid-neglecting contacting scheme.

The change between both measurements is then affected by the different state (host vs. cut) and the different contacting (grid neglecting vs. grid including). Using Gridmaster+, the difference in the experimental data can be separated between both effects. It should be noted that the current flow using grid-including contacting in I–V testing is closer to the current flow on module level, where the current is passed along the short side of a shingle through the whole length of a finger. Comparing a grid-neglecting host measurement to the final module performance would therefore give an unreasonably high CTM loss.

A similar systematic difference is present, when comparing multi-busbar and shingle layouts. For (multi-)busbar interconnection, the current is passed through the fingers until it reaches the closest busbar, which is contacted by a (highly conductive) ribbon in the module. The maximum distance for current transport in the fingers is therefore half of the width of the busbar distance. For shingle interconnection, the current transport in the fingers is about the whole length of the shingle cell. This difference is included in the simulation of the cell performance (Gridmaster+) as well as on the module performance (SmartCalc.Module).

All described effects are lumped in the efficiency. The shingle hosts have a larger shading due to the wider grid lines, and therefore lower ISC on the same host cell area. The difference in grids (and current flow) is also reflected in lower VOC and FF. As the efficiency is an area-normalized quantity, the change in ISC due to cutting is not reflected here. The grid-neglecting measurements indicate a higher performance than the grid-including measurements, which are closer to the situation on module level. Considering this, the half-cell layout gives a host efficiency of 21.7%, while the shingle layout achieves 20.8%.

Cutting the cells results in a decreased performance for both half (21.6%) and shingle cells (20.3%), although the effect is much more pronounced for shingles (–0.5%) with their higher edge-to-area ratio. Removing the edge recombination by adding a passivation can recover this loss and bring the cells back close to their host level efficiency. The presented comparisons should be seen as general trends, but the listed numbers are specific to the precursors and processes (including grid-layouts) chosen for this experiment. The absolute values are therefore not a general finding for shingle or half-cell technology. This will be further discussed in the next section.

thumbnail Fig. 2

Experimental (symbols) and simulated (bars) I–V parameters for the implemented half-cell and shingle cell grid layouts on the same industrial precursors.

4.2 Simulation-based optimization of shingle grids

The demonstrated and validated implementation of precursor and cell parameters into Gridmaster+, can be used to virtually optimize the resulting cell parameters. One obvious optimization, which has also been demonstrated in the past by others [15,17], is the number of front side Ag fingers, to balance the tradeoff between optical and electrical losses3. It should be noted that electrical losses simulated in Gridmaster+ include ohmic losses in the grid for current transport from one edge to the other, as well as metal-induced recombination. As mentioned earlier, a higher number of fingers compared to multi-busbar half-cells is expected due to the prolonged current paths. Another optimization is the shingle stripe width, i.e. the number of cuts per host cell (s. also [16,17]). While shorter stripes reduce the ohmic finger losses, the edge to area ratio is increased, increasing the recombination losses in the presence of edge recombination. Resulting cut cell efficiencies for 1/5th (33.2 mm width), 1/6th (27.7  mm) and 1/7th (23.7) cut shingle cells with and without edge recombination are shown as a function of the number of front side Ag fingers in Figure 3. The results are simulated assuming a pin-like contacting, therefore including the ohmic losses in the grid, as relevant for the module integration.

The dashed lines at the bottom indicate the trends for cells suffering from edge recombination on both cut edges. The vertical grey line indicates the implemented number of front side Ag fingers in the experiment (128). According to the simulation, a higher number of fingers would result in a better balance between electric and optical losses, however the increase in efficiency is Δη < 0.1%abs. Also, the 1/7th cut cell is worse, due to the aforementioned increased effect of edge recombination. For 1/5th and 1/6th the effects coincidentally level out in the presented case.

The full lines at the top show the situation, where edge recombination is switched off in the simulation. Here, the dominating effect is the shorter current paths in smaller stripes and therefore reduced ohmic losses, putting the 1/7th cells at the top. As seen before, this has a much stronger effect than the optimization of the grid layout, with Δη = 0.5%abs. to 0.8%abs.

Still an increase of the number of fingers would result in a higher efficiency. It should be noted that for practical reasons not only the power output per cell but also the cost per cell need to be optimized and that a higher number of Ag fingers results in higher consumable costs. Interestingly, the optimum number of fingers without edge recombination is 6–7 fingers (∼3%rel.) lower than in the case with edge recombination, due to the more pronounced effect of metal-induced recombination.

Further optimization of shingle solar cell hosts and cut cells would be possible by adjusting other precursor properties (such as emitter sheet resistance, surface passivation etc.), which has not been addressed in this work, but is generally possible with a simulation tool like Gridmaster+.

thumbnail Fig. 3

Cut cell efficiencies for 1/5th, 1/6th and 1/7th cut shingle cells with and without edge recombination as a function of the number of front side Ag fingers simulated with the same precursor properties. The results are simulated including full grid contribution (pin-like contacting).

4.3 Simulated module performance

The performance of the host and cut cells have been taken as the basis for a CTM-calculation using SmartCalc.Module. To show the advantage of using cut cells, modules with full cells (FC), half-cut (HC) cells, 1/5th-, 1/6th-, and 1/7th-cut shingle cells have been simulated.

For all simulations, the same BOM has been chosen to make the results comparable (3.2 mm thick glass, ethylene vinyl acetate encapsulant, white backsheet, solder-coated copper ribbons or electrically conductive adhesive). The parameters of all materials are derived from commercially available products.

The module geometries are chosen derived from commercial M6-PERC-modules with 120 half cells and our internal module designs optimized for shingle modules. All modules are simulated with an aluminum frame of 13 mm width and 10 mm overlap to the glass. For all modules the outer margin from edge to cell matrix is 14.5 mm on the left and right. For full and half-cell modules the top and bottom margin is 29.7 mm, while it is 17.5 mm for the shingle modules. The cell gap for full and half-cells is 1 mm, while the overlap of shingles is 0.9 mm. The string distance for full and half-cells is 1.5 mm, while it is 0.5 mm for shingles. The number of shingles per string has been chosen depending on the shingle width, to match the length of the other modules. In the end, the HC module (120 half cells) has a size of 1744 mm × 1038 mm. The FC module (60 full cells) is 1734 mm × 1038 mm. The shingle modules are 1752 mm × 1033 mm (318 1/5th- shingle cells), 1753 mm × 1033 mm (384 1/6th- shingle cells), and 1750 mm ×1033 mm (450 1/7th- shingle cells).

As shown in previous work [28], the cut cells (half-cells, resp. shingle) benefit from the lower current and therefore lower ohmic losses compared to the full resp. larger cells, which results in lower CTM losses. The efficiency ratio CTMη is given as CTMη = ηModule/ηCell. In this work, we have simulated the module efficiency ηModule for different shingle sizes and calculated the efficiency ratio CTMη, for the efficiencies ηCell of cells with optimized grids as described in the last section, as well as fixed grids with 128 front side Ag fingers, and with and without edge passivation. For this, we used an updated version of SmartCalc.Module compared to our previous work, which results in slightly different results. In general, it should be noted that the cell-to-module simulation has a strong dependency on the design choices made for the module4. The differences between the simulations performed in this work are ΔCTMη < 0.1%abs. We therefore show the mean CTMη for the different module types in Table 1.

For the selected module designs, advantages in CTMη are demonstrated for cut cells compared to full cells, as described above. Moreover, it is shown for the shingle modules, which are well comparable due to their very similar designs, that the advantages of overlapping interconnection are increasing with decreasing shingle widths. However, considering Figure 3, the cell efficiency of smaller cells are more affected by edge recombination, which can then result in overall lower module efficiency. To realize the potential gain indicated by the CTM-simulation, it is therefore important to maximize the cut-cell efficiency.

The simulated CTMη values can also be used to better understand the feasible difference between two different types of host cells. As an example, one might want to achieve ηShingle−Module ≥ ηHC−Module. Inserting the definition of CTMη here, gives

Using the CTMη from Table 1, this means that 1/5th cut shingle cells can only be 1.7%rel. worse than half-cut cells, while 1/7th cut shingles could be up to 4.0%rel. worse and still achieve the same module efficiency (due to the higher CTMη).

Again, it is important to note that these results illustrate the general trends and pathways for optimization, but absolute numbers are only valid for the given selections of parameters.

Table 1

Module sizes and mean cell-to-module ratio for different cell types.

5 Conclusion

This study investigates the challenges and advantages of utilizing cut solar cells for shingling and half-cell modules. Using a combined simulation framework based on Gridmaster+ and SmartCalc.Module, as well as experimental results, several key aspects could be demonstrated.

Edge recombination in cut cells is much more pronounced in the case of shingle cells due to the higher edge-to-area ratio. This highlights the importance of addressing cutting-induced losses in shingle modules. The application of passivated edge technology (PET) was experimentally explored, proving to recover cutting-induced losses, and improving the electrical performance of shingle modules.

The choice of contacting scheme for I–V measurements was found to be crucial for accurate comparisons between the host and the cut cell state. While grid-neglecting contacting, like GridTOUCH®, provides flexibility in R&D settings, it can lead to an overestimation of the host performance and suggest higher CTM losses.

While cut cells have been established due to their advantage on module level, shingling layouts have the potential to further improve the module performance based on the same precursor processes, when a suitable edge passivation after cutting can be employed. Crucially, this is demonstrated to be possible, even when the host cell performance of shingles is lower than that of half-cells, as long as a higher CTM ratio can be realized with shingle modules.

Acknowledgements

We would like to express our gratitude to our colleagues at Fraunhofer ISE for their valuable contributions and support throughout this research project, especially Tobias Fellmeth, Puzant Baliozian, Gernot Emanuel, Diana Witt, Marc Retzlaff, Milad Salimi Sabet, Felix Maischner, and Alexander Krieg. Their expertise and support were instrumental in the successful execution of the experimental work.

Funding

We would also like to acknowledge the funding provided by the Federal Ministry for Economic Affairs and Climate Action (BMWK) through the project “Guten-Morgen” (FkZ: 03EE1101A).

Conflicts of interest

Authors declare no conflict of interest.

Data availability statement

Data can be made available upon reasonable request.

Author contribution statement

J.D.H. lead the research project and coordinated the main experimental and simulative work. E.L. supported the design of experiment, application and evaluation of PET processes and data analysis. T.R. and D.v.K. set up the module simulations using SmartCalc.Module. B.S. and C.R. updated the Gridmaster+ simulation tool. J.W., N.A.L., and T.R. provided support on the shingle and half-cell grid layouts and module implementation. M.H. supported the implementation, analysis, and optimization of Passivated Edge Technology (PET). A.K., H.N., F.C., and R.P. provided support in funding acquisition, project coordination and overall know-how. All authors reviewed and edited the manuscript.

References

  1. S. Guo, J.P. Singh, I.M. Peters et al., A quantitative analysis of photovoltaic modules using halved cells, Int. J. Photoenergy 2013, 1 (2013). https://doi.org/10.1155/2013/739374 [Google Scholar]
  2. ITRPV, International Technology Roadmap for Photovoltaic (ITRPV): 2023 Results, 14th Edition (ITROV, 2023) [Google Scholar]
  3. P. Baliozian, N. Klasen, N. Wöhrle et al., PERC-based shingled solar cells and modules at Fraunhofer ISE, Photovolt. Int. 43, 129 (2019) [Google Scholar]
  4. N. Wöhrle, T. Fellmeth,E. Lohmüller et al., The SPEER solar cell − simulation study of shingled PERC technology based stripe cells, in 33rd European Photovoltaic Solar Energy Conference and Exhibition. Proceedings (2017), pp. 844–848 [Google Scholar]
  5. H. Schulte-Huxel, A. Kraft, T. Roessler et al., Chapter 10: Module interconnection technologies, in Silicon Solar Cell Metallization and Module Technology, edited by T. Dullweber, L. Tous (IET, 2021), pp. 435–489 [CrossRef] [Google Scholar]
  6. D. Tune, T. Rössler, G. Oreski et al., The sun is rising on conductive adhesives, Photovolt. Int. 47, 57 (2022) [Google Scholar]
  7. N. Klasen, A. Mondon, A. Kraft et al., Shingled cell interconnection: a new generation of bifacial PV-modules, in 7th Workshop on Metallization & Interconnection for Crystalline Silicon Solar Cells (2017) [Google Scholar]
  8. M. Mittag, T. Zech, M. Wiese et al., Cell-to-Module (CTM) analysis for photovoltaic modules with shingled solar cells, in 44th IEEE Photovoltaic Specialists Conference (PVSC). Conference Record (2017), pp. 1531–1536 [Google Scholar]
  9. D. Tonini, G. Cellere, M. Bertazzo et al., Shingling technology for cell interconnection: technological aspects and process integration, in 33rd European Photovoltaic Solar Energy Conference and Exhibition. Proceedings (2017), pp. 38–41 [Google Scholar]
  10. N. Wöhrle, E. Lohmüller, M. Mittag et al., Solar cell demand for bifacial and singulated-cell module architectures, Photovolt. Int. 36, 48 (2017) [Google Scholar]
  11. V. Giglia, J. Veirman, R. Varache et al., Influence of edge recombinations on the performance of half-, shingled- and full silicon heterojunction solar cells, in 37th European Photovoltaic Solar Energy Conference and Exhibition (2007), pp. 282–285 [Google Scholar]
  12. M. Bokaličc, M. Kikelj, B. Lipovšek et al., Insights into cut-edges of SHJ solar cells by EL and LBIC characterization, in 8th World Conference on Photovoltaic Energy Conversion (2022), pp. 63–66. https://doi.org/10.4229/WCPEC-82022-1BO.4.6 [Google Scholar]
  13. N. Chen, D. Tune, F. Buchholz et al., Impact of cut edge recombination in high efficiency solar cells − measurement and mitigation strategies, in 38th European Photovoltaic Solar Energy Conference and Exhibition (2021), pp. 253–256. https://doi.org/10.4229/EUPVSEC20212021-2CV.1.12 [Google Scholar]
  14. N. Bassi, C. Clerc, Y. Pelet et al., GridTOUCH: Innovative solution for accurate IV measurement of busbarless cells in production and Laboratory Environments, in 29th European Photovoltaic Solar Energy Conference and Exhibition Proceedings (2014), pp. 1180–1185 [Google Scholar]
  15. D. Rudolph, J. Rabanal-Arabach, I. Ullmann et al., Cell design optimization for shingled modules, in 33rd European Photovoltaic Solar Energy Conference and Exhibition (2017), pp. 880–883. https://doi.org/10.4229/EUPVSEC20172017-2CV.2.44 [Google Scholar]
  16. S. Harrison, A. Bettinelli, B. Portaluppi et al., Challenges for efficient integration of SHJ based solar cells in shingle module configuration, in 37th EU PVSEC (2020), pp. 223–227 [Google Scholar]
  17. W. Oh, J. Park, C. Jeong et al., Design of a solar cell electrode for a shingled photovoltaic module application, Appl. Surf. Sci. 510, 145420 (2020). https://doi.org/10.1016/j.apsusc.2020.145420 [CrossRef] [Google Scholar]
  18. D. von Kutzleben, T. Roessler, M. Mittag et al., Development of shingle matrix technology for integrated PV applications, in 8th World Conference on Photovoltaic Energy Conversion (2022), pp. 541–550. https://doi.org/10.4229/WCPEC-82022-3CO.4.4 [Google Scholar]
  19. B. Shabanzadeh, Modeling of Photovoltaic Modules by Evaluating Silicon and Tandem Solar Cells. Master thesis, Albert-Ludwigs-University, 2023 [Google Scholar]
  20. M. Mittag, Systematic PV-module optimization with the cell-to-module (CTM) analysis software “SmartCalc. CTM”, Photovolt. Int. 36, 97 (2017) [Google Scholar]
  21. T. Fellmeth, F. Clement, D. Biro, Analytical modeling of industrial-related silicon solar cells, IEEE J. Photovolt. 4, 504 (2014). https://doi.org/10.1109/jphotov.2013.2281105 [CrossRef] [Google Scholar]
  22. A. Fell, J. Schön, M. Müller et al., Modeling edge recombination in silicon solar cells, IEEE J. Photovolt. 8, 428 (2018). https://doi.org/10.1109/JPHOTOV.2017.2787020 [CrossRef] [Google Scholar]
  23. M. Mittag, Systematic PV-module optimization with the cell-to-module (CTM) analysis software “SmartCalc. CTM”, Photovolt. Int. 36, 97 (2017) [Google Scholar]
  24. R. Preu, J. Rentsch, S. Rein et al., Lessons learned from 25 years production technology research & development, in 8th World Conference on Photovoltaic Energy Conversion (2022), pp. 1–6. https://doi.org/10.4229/WCPEC-82022-1CP.2.1 [Google Scholar]
  25. A. Münzer, P. Baliozian, K. Ahmed et al., Laser assisted separation processes for bifacial pSPEER shingle solar cells, in 37th European Photovoltaic Solar Energy Conference and Exhibition. Proceedings (2020), pp. 394–399 [Google Scholar]
  26. P. Baliozian, M. Al-Akash, E. Lohmüller et al., Postmetallization “passivated edge technology” for separated silicon solar cells, IEEE J. Photovolt. 10, 390 (2020). https://doi.org/10.1109/JPHOTOV.2019.2959946 [CrossRef] [Google Scholar]
  27. S. Eiternick, F. Kaule, H.-U. Zühlke et al., High quality half-cell processing using thermal laser separation, Energy Proc. 77, 340 (2015). https://doi.org/10.1016/j.egypro.2015.07.048 [CrossRef] [Google Scholar]
  28. J.D. Huyeng, E. Lohmüller, T. Rößler et al., Challenges and advantages for cut solar cells for shingling and half-cell modules, in 40th European Photovoltaic Solar Energy Conference and Exhibition, WIP, Munich (2023). https://doi.org/10.4229/EUPVSEC2023/1BV.5.42 [Google Scholar]
1

“Gridmaster+” further includes the option to simulate tandem cells, which is not used in this work.

2

It should be noted that the number of available input parameters is much larger than the number of experimentally determined output parameters, leaving room for additional systematic uncertainty. We therefore assume a conservative estimation of ± 2%rel. for the accuracy of the results.

3

Please note that the simulation here is performed on “cell level”, i.e. the optical optimization is not considering for example finger reflections inside the module stack (glass/air interface), which can shift the results.

4

One dominant parameter that has been optimized for industrial modules in terms of efficiency in the past years, is the wafer format and number of cells per module. One should therefore keep in mind that these simulations have been based on M6-size wafers and module dimensions corresponding to 120 half-cut PERC cells, when comparing to commercial products.

Cite this article as: Jonas D. Huyeng, Elmar Lohmüller, Behnaz Shabanzadeh, Christian Reichel, Torsten Rößler, Julian Weber, Marc Hofmann, Daniel von Kutzleben, Najwa Abdel Latif, Achim Kraft, Holger Neuhaus, Florian Clement, Ralf Preu, Challenges and advantages of cut solar cells for shingling and half-cell modules, EPJ Photovoltaics 15, 22 (2024)

All Tables

Table 1

Module sizes and mean cell-to-module ratio for different cell types.

In the text

All Figures

thumbnail Fig. 1

Photographs of bifacial PERC solar host cells with half-cell (left) and shingle metallization (right) cell layout, fabricated on the same industrial precursors in M6 wafer format at Fraunhofer ISE PV-TEC Back-End laboratory. © Fraunhofer ISE.
In the text
thumbnail Fig. 2

Experimental (symbols) and simulated (bars) I–V parameters for the implemented half-cell and shingle cell grid layouts on the same industrial precursors.
In the text
thumbnail Fig. 3

Cut cell efficiencies for 1/5th, 1/6th and 1/7th cut shingle cells with and without edge recombination as a function of the number of front side Ag fingers simulated with the same precursor properties. The results are simulated including full grid contribution (pin-like contacting).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.