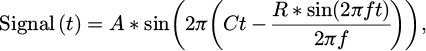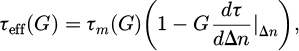| Issue |
EPJ Photovolt.
Volume 14, 2023
Special Issue on ‘WCPEC-8: State of the Art and Developments in Photovoltaics’, edited by Alessandra Scognamiglio, Robert Kenny, Shuzi Hayase and Arno Smets
|
|
|---|---|---|
| Article Number | 19 | |
| Number of page(s) | 5 | |
| Section | Modules and Systems | |
| DOI | https://doi.org/10.1051/epjpv/2023010 | |
| Published online | 17 May 2023 | |
https://doi.org/10.1051/epjpv/2023010
Regular Article
In situ minority carrier lifetime via fast modulated photoluminescence
1
Institut Photovoltaïque d'Ile-de-France (IPVF), 18 Bvd Thomas Gobert, 91120 Palaiseau, France
2
LPICM, CNRS, Ecole Polytechnique, Institut Polytechnique de Paris, route de Saclay, 91128 Palaiseau, France
* e-mail: mateusz.poplawski@ipvf.fr
Received:
31
July
2022
Received in final form:
22
October
2022
Accepted:
30
January
2023
Published online: 17 May 2023
Modulated photoluminescence (MPL) is a powerful technique for determining the effective minority carrier lifetime (τeff) of semiconductor materials and devices. MPL is based on the measurement of phase shifts between two sinusoidal waves (minimal amplitude excitation; and PL signal). In particular, in situ τeff has been proven to be an effective measurement at showing changes within a plasma-enhanced chemical vapor deposition reactor during fabrication of c-Si solar cells. However, the required time for a single measurement, using the previous method, was 40 s. In this paper a new input signal is proposed, called Dolphin's Wave, providing a method for decreasing the required measurement period to under 2 s, using superposition, frequency sweeps, and wavelets.
Key words: In situ lifetime / modulated photoluminescence / silicon / AlOx / Lissajous curves
© M. Poplawski et al., Published by EDP Sciences, 2023
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
With the development of photovoltaic market to the Terawatt level, the quality control during manufacturing is a key issue requiring further research as it can help to increase the efficiency of the devices as well as their production yield. Current aims for c-Si solar cell research always target continuous increase in solar cell efficiency, while increasing production throughput up to 15,000 wafers per hour (4.2 per second), which sets challenges for inline control equipment [1]. Effective minority carrier lifetime (τeff) has been shown as a good indicator for the quality of a photovoltaic cell precursor when performed in between fabrication stages during manufacturing [2,3]. To further increase effectiveness, τeff measurements must be done where it is currently not, meaning in situ is required. In situ τeff measurements have been used to show hidden dynamics of minority carriers in a silicon wafer during annealing with successful results [4–7]. The standard method is to use the τeff value at a carrier density of 1015 cm−3 to link with the standard operating conditions of a solar cell [3]. Variation in the illumination intensity profile, using analytical solutions, has resulted in previous very successful τeff measurement devices by Sinton (QSSPC), Fraunhofer ISE (Self Consistent Determination (SCD)), and BTI Imaging (Photoluminescent Imaging) [8–10].
Modulated photoluminescence (MPL) is a contactless method that can be used to determine the τeff of a photovoltaic cell via measuring phase shifts between an excitation signal (laser beam) and an emitted photoluminescence signal [11]. Traditionally MPL is performed using multiple standing sinusoidal frequencies, and light intensities, to determine the phase shifts generated at multiple carrier densities from a semiconductor sample, after which correction formulas are applied to determine the τeff [4–7,10–13].
It has also been applied for use in determining defects in Cu(In,Ga)Se which is a thin films photovoltaics material and in Fluorescence lifetime imaging [12,13].
τeff measurements have been widely applied to a wide range of materials, in particular aluminum oxide (AlOx). It is the focus of numerous research teams, for its excellent surface passivation quality with crystalline silicon [14]. It has been applied to current and new solar cell architectures such as passivated emitter and rear contact, tunnel oxide passivated contacts, and heterojunction [15–17]. Being heavily researched throughout the years and currently being developed via high throughput ALD techniques, it is clear this material holds promise [18]. AlOx films usually provide weak passivation in their as-deposited state and require annealing to activate the formation of a high density of negative fixed charge which improves the field effect passivation.
The light soaking effect is one which constant illumination can either induce degradation or improve a sample depending on the material type [19,20]. AlOx was shown to improve due to light soaking via increasing the field effect passivation that occurs through the creation of an inversion layer at the cSi/AlOx, which could potentially allow higher lifetimes to be achieved during production [6]. A trapping and detrapping model where the electrons tunnel through the interface into traps within the AlOx layer has been used to describe the mechanism [21].
In this work, an input signal is presented on how to increase the phase shift measurement speed between two minimal amplitude sinusoidal waves and across various light intensities using superposition, frequency sweeps, and wavelets. The unique features of this technique are illustrated by a study of the effects of light-soaking on the field effect passivation provided by AlOx films.
2 Method
The Plasma-Enhanced Chemical Vapor Deposition (PECVD) reactor being used has been previously described with an in situ MPL system using a lock-in amplifier to determine the phase shift of a standing sinusoidal wave, including the data processing stage after phase shift extraction for τeff [4,6]. The system has been modified by replacing the lock-in amplifier (Princeton Instrument SR-830) with a voltage function generator/data logger (DT9847 Series) set at 30 kHz acquisition rate. The applied laser signal and photoluminescence signal are recorded and sent to a MATLAB app. Within MATLAB, signal processing was performed before using the wavelet coherence function [22]. Wavelet transforms allow for frequency, time, and information to be extracted from a signal, in this case phase shift. The DT9847 function generator was used to apply a custom input signal, to the laser diode controller (ICT4001 Thorlabs) controlling a 785 nm laser diode (LP785-SF100), creating a collimated 8 mm diameter top hat beam which illuminates the back of the sample within the PECVD reactor. The emitted photoluminescence is collected via an optical setup focusing onto an InGaAs photodiode (FGA10 Thorlabs, Fig. 1). A FZ N-type silicon wafer, initially cleaned with hydrofluoric acid, with both sides coated with 9 nm ALD AlOx at 150 °C was used throughout the entire process [7].
 |
Fig. 1 Schematic of the setup mounted on a PECVD reactor combining in situ PL. Optics diagram shown in [7]. |
3 Results
The initial assumption made for MPL is the approximation where a wave of miniscule amplitude is equal to a straight line as to not create a noticeable perturbation [11]. When generating a standing wave using a digital to analog conversion device, the number of points per second used to define the wave must be stated. These points will all relate to an instantaneous frequency within the generated wave (Fig. 2).
In digital signal processing, a waveform can be represented as a series of discrete points generated at regular intervals in time. By adjusting the amplitude (intensity) values at each point, the instantaneous frequency of the waveform can be modified, allowing for representation of different pieces of information for each point in time (cf. Fig. 3, Eq. (1)).
A frequency sweep is implemented by modifying the angular rotation of a standing wave giving a range from a core frequency. The implementation uses a sinusoidal wave for changing the instantaneous frequency from 10 to 70 Hz using a core frequency of 40 Hz with range of 30 Hz at a 0.5 Hz sweep rate. Given the applied wave is equal to a set of dissociated points in time, variation of the measurement duration should have no effect on the results.
A = amplitude, C = core frequency (Hz), R = range (Hz), f = sweep frequency (Hz).
The measured phase shifts (Fig. 4), using a frequency sweep from 100 to 700 Hz in duration from 2 to 10 s, with 2 s steps, each show the same values with all points being unique from their neighbours. This aligns well with the initial MPL assumption made. The phase shift was extracted via performing a wavelet coherence transform in MATLAB with the standard settings provided. This solves the first MPL hurdle of slow phase shift measurements at a single excess carrier density. The limitation of how fast a frequency sweep can be performed is directly related to the maximum acquisition rate capable. Such concepts have already been applied in impedance spectroscopy [23,24].
The second issue to solve regarding MPL is acquiring the phase shift across multiple excess carrier densities quickly. In contrast to applying a small amplitude wave to determine the τeff, a large single frequency sinusoidal wave, covering the entire excess carrier density (light intensity) range desired, may be applied to determine an effective electron lifetime via SCD. SCD relies upon induced hysteresis due to a fast rate of change in the carrier density based on the illumination intensity [9]. The issue is solved by doing the opposite of SCD where the change in light intensity is kept to a minimum in order to not create a noticeable perturbation within the system. From this comes Dolphin's Wave (Fig. 5) where a frequency sweep is superimposed onto a low frequency standing wave. Due to each point in time being unique, phase shifts with a combination of frequencies and excess carrier densities are created. The base wave being 5.3 Hz with an amplitude of 100 mV, while the sweep has a frequency range from 100 to 700 Hz with a sweep frequency of 3 Hz and an amplitude of 20 mV.
Figure 6 compares three phase shift values (blue points) determined via using a lock in amplifier (at 0.15 mA, measured in 7 s), to a snapshot of ∼5000 phase shifts (red points) measured, at 0.15 ± 0.05 mA, in 0.05 s out of 0.2 s. A fitted line further shows that Dolphin's wave and the standing wave method both produce the same results. This is further illustrated in Figure 7 which provides a comparison between a full measurement using a standing wave and Dolphin's Wave which represents a Lissajous curve due to the construction of the wave. The previous system (based on standing waves), required 40 s for 18 phase shifts obtained by varying both the laser current and the frequency, one value at a time. In comparison Dolphin's Wave measured 60,000 phase shifts in 2 s, which is based on the 30 kHz acquisition rate. Thus, an example for MPL using Dolphin's Wave for a fast phase shift extraction method is presented which has been successful to 0.25 s for a measurement.
The increase in speed is attributed to removing the need to record more than 1 point per frequency/phase shift with the use of wavelets and a frequency sweep. If using a lock-in amplifier or short term Fourier transform, more points at a given instantaneous frequency are required to extract a reliable phase shift for the given frequency.
To calculate a minority carrier lifetime spectrum, equation (2) is applied to Figure 7 in multiple segments, as shown in Figure 6, to calculate a series of τm which then need to be corrected to τeff using equation (3). A more detailed explanation can be found here [2,6,13].
τm = modulated lifetime, ɸ = phase shift based on frequency, ω = frequency (radians).
τeff = Corrected lifetime, G = generation rate, n = carrier concentration.
To demonstrate the effectiveness/stability of the newly proposed input wave, an AlOx light soaking experiment was performed at room temperature. Figure 8 shows the τeff (1015 cm3) measured at room temperature on an as-deposited AlOx sample. During the measurement the sample was light-soaked by the 785 nm laser diode with an average power of 20 mW/cm2. The continuous τeff measurement was performed for ∼2.5 h with the lifetime recorded every 2 s at an excess carrier density of 1015 cm−3. The repeatability of the measurements can be seen due to the slow increase of τeff allowing for a large number of measurements to be taken at a given value without significant deviation occurring demonstrating the repeatability and accuracy. The slight jumps/large bumps throughout the measurement are due to the internal clock for the data logger not starting at the same time for each measurement.
A box plot (Fig. 9) is used to provide a simple and easily interpretable representation of the central tendency, dispersion, and skewness. Three periods of 40 s intervals were chosen at 3750 s, 4810 s, and 5880 s to compare the reliability of the method. The interquartile range being ∼3 μs allowing for a clear trend to be determined over a small change in the lifetime value of a sample.
 |
Fig. 2 Depiction of the instantaneous frequency in relation to its standing wave. |
 |
Fig. 3 Top showing the instantaneous frequency of a frequency sweep with the bottom showing the actual signal. |
 |
Fig. 4 Measured phase shifts using the signal described in Figure 3 showing the dissociation between points in time. |
 |
Fig. 5 Dolphin's Wave constructed using a small amplitude (20 mV) frequency sweep (100–700 Hz at 3 Hz) super imposed onto a large amplitude (100 mV) low frequency (5.3 Hz) standing wave. |
 |
Fig. 6 Comparison of standing & Dolphin's wave showing 3 phase shifts at 0.15 mA acquired in 7 s and ∼5000 phase shifts at 0.15 mA ± 0.05 in 0.2 s. |
 |
Fig. 7 Comparison of standing and Dolphin's wave methods showing 18 phase shifts acquired in 40 s vs 60,000 phase shifts in 2 s. |
 |
Fig. 8 Light-soaking of the AlOx sample at room temperature over a period of ∼2.5 h showing an increase of 60 μs with measurements every 2 s. |
4 Conclusion
A new method has been presented allowing an increase in speed for performing a real time τeff measurement via MPL. Dolphin's wave superimposing a small amplitude frequency sweep onto, an out of sync, a large amplitude low frequency standing wave allowed for decreased times for phase shift extraction. The lowest measurement duration of 0.25 s successfully fulfilled the requirements for the production throughput target of 4.2 wafers/s. An example of in situ τeff measurements using AlOx light soaking effects was used to demonstrate the repeatability and accuracy of the method successfully.
Acknowledgments
The authors thank Pavel Bulkin for providing the AlOx samples with which the work was done.
Author contribution statement
Mateusz Poplawski: − Conceptualization, Investigation, Validation, Visualization, Software, Writing − original draft, Writing − review & editing. François Silva: − Resources, Conceptualization. Jean-Charles Vanel: − Resources, Hardware. Pere Roca i Cabarrocas: − Supervision, Project administration, Writing − review & editing.
References
- High speed processing on large wafers with newly developed on-the-fly laser equipment − Fraunhofer Ise, 2022 (private communication) [Google Scholar]
- A. Cuevas, D. Macdonald, Sol. Energy 76, 255 (2004) [CrossRef] [Google Scholar]
- R.A. Sinton, A. Cuevas, M. Stuckings, in Proceedings of the Twenty Fifth IEEE Photovoltaic Specialists Conference (IEEE, 1996), pp. 457–460 [Google Scholar]
- M. Sreng, Ph.D. thesis, Ecole Polytechnique (2019) [Google Scholar]
- A. Desthieux, M. Sreng, P. Bulkin, I. Florea, E. Drahi, B. Bazer-Bachi, J.-C. Vanel, F. Silva, J. Posada, P. Roca i Cabarrocas, Sol. Energy Mater. Sol. Cells 230, 111172 (2021) [CrossRef] [Google Scholar]
- M. Sreng, F. Silva, P. Roca i Cabarrocas, Phys. Stat. Solidi 216, 1800612 (2019) [Google Scholar]
- S.N. Abolmasov, P. Roca i Cabarrocas, J. Vacuum Sci. Technol. A 33, 021201 (2015) [CrossRef] [Google Scholar]
- T. Trupke, R.A. Bardos, Appl. Phys. Lett. 85, 3611 (2004) [CrossRef] [Google Scholar]
- T. Trupke, R.A. Bardos, M. Abbott, E. Pink, Y. Augarten, F.W. Chen, K. Fisher, J.E. Cotter, M. Kasemann, M. Rüdiger, S. Kontermann, M. Schubert, M. The, S. Glunz, W. Warta, P. Wuerfel, D. Macdonald, J. Tan, A. Cuevas, J.M. Fernandez, in Proceedings of the 22nd European Photovoltaic Solar Energy Conference (2007), pp. 22–31 [Google Scholar]
- J.A. Giesecke, S.W. Glunz, W. Warta, J. Appl. Phys. 113, 073706 (2013) [CrossRef] [Google Scholar]
- R. Brüggemann, S. Reynolds, J. Non-Cryst. Solids 352, 1888 (2006) [CrossRef] [Google Scholar]
- B. Bérenguier, N. Barreau, A. Jaffré, D. Ory, J.F. Guillemoles et al., Thin Solid Films 669, 520 (2019) [PubMed] [Google Scholar]
- J.R. Lakowicz, B.P. Maliwal, Biophys. Chem. 21, 61 (1985) [Google Scholar]
- J. Schmidt, F. Werner, B. Veith, D. Zielke, S. Steingrube, P.P. Altermatt, S. Gatz, T. Dullweber, R. Brendel, Energy Procedia 15, 30 (2012) [CrossRef] [Google Scholar]
- D. Tröger, M. Grube, J. Lehnert, T. Mikolajick, Sol. Energy Mater. Sol. Cells 215, 110651 (2020) [CrossRef] [Google Scholar]
- B.W.H. van de Loo, B. Macco, M. Schnabel, M.K. Stodolny, A.A. Mewe, D.L. Young, W. Nemeth, P. Stradins, W.M.M. Kessels, Sol. Energy Mater. Sol. Cells 215, 110592 (2020) [CrossRef] [Google Scholar]
- Y.-H, Lin, Y.-C. Wu et al., Energies 7, 3653 (2014) [Google Scholar]
- J. Melskens, B.W.H. van de Loo, B. Macco, M.F.J. Vos, J. Palmans, S. Smit, W.M.M. Kessels, in Proceedings of the 42nd Photovoltaic Specialist Conference (PVSC) (IEEE, 2015) [Google Scholar]
- M. Gostein, L. Dunn, in Proceedings of the 37th IEEE Photovoltaic Specialists Conference (2011) [Google Scholar]
- F. Lebreton, Ph.D. thesis, Universite Paris-Saclay (2017) [Google Scholar]
- M. Xie, X. Yu, X. Qiu, D. Yang, Sol. Energy Mater. Sol. Cells 191, 350 (2019) [CrossRef] [Google Scholar]
- A. Grinsted, J.C. Moore, S. Jevrejeva, Nonlinear Process. Geophys. 11, 561 (2004) [CrossRef] [Google Scholar]
- W. Li, Q.-A. Huang, C. Yang, J. Chen, Z. Tang, F. Zhang, A. Li, L. Zhang, J. Zhang, Electrochim. Acta 322, 134760 (2019) [CrossRef] [Google Scholar]
- R. Suresh, S. Swaminathan, R. Rengaswamy, Int. J. Hydrogen Energy 45, 10536 (2020) [CrossRef] [Google Scholar]
Cite this article as: Mateusz Poplawski, François Silva, Jean-Charles Vanel, Pere Roca i Cabarrocas, In situ minority carrier lifetime via fast modulated photoluminescence, EPJ Photovoltaics 14, 19 (2023)
All Figures
 |
Fig. 1 Schematic of the setup mounted on a PECVD reactor combining in situ PL. Optics diagram shown in [7]. |
| In the text | |
 |
Fig. 2 Depiction of the instantaneous frequency in relation to its standing wave. |
| In the text | |
 |
Fig. 3 Top showing the instantaneous frequency of a frequency sweep with the bottom showing the actual signal. |
| In the text | |
 |
Fig. 4 Measured phase shifts using the signal described in Figure 3 showing the dissociation between points in time. |
| In the text | |
 |
Fig. 5 Dolphin's Wave constructed using a small amplitude (20 mV) frequency sweep (100–700 Hz at 3 Hz) super imposed onto a large amplitude (100 mV) low frequency (5.3 Hz) standing wave. |
| In the text | |
 |
Fig. 6 Comparison of standing & Dolphin's wave showing 3 phase shifts at 0.15 mA acquired in 7 s and ∼5000 phase shifts at 0.15 mA ± 0.05 in 0.2 s. |
| In the text | |
 |
Fig. 7 Comparison of standing and Dolphin's wave methods showing 18 phase shifts acquired in 40 s vs 60,000 phase shifts in 2 s. |
| In the text | |
 |
Fig. 8 Light-soaking of the AlOx sample at room temperature over a period of ∼2.5 h showing an increase of 60 μs with measurements every 2 s. |
| In the text | |
 |
Fig. 9 Box plots of 3 40 s periods highlighted in Figure 8 by yellow boxes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.