| Issue |
EPJ Photovolt.
Volume 8, 2017
Topical Issue: Theory and modelling
|
|
|---|---|---|
| Article Number | 85505 | |
| Number of page(s) | 12 | |
| Section | Theory and modelling | |
| DOI | https://doi.org/10.1051/epjpv/2017006 | |
| Published online | 01 August 2017 | |
https://doi.org/10.1051/epjpv/2017006
On the ab initio calculation of vibrational formation entropy of point defect: the case of the silicon vacancy
1 Institut Photovoltaïque d’Ile-de-France (IF), 8, rue de la Renaissance, 92160 Antony, France
2 Institute for Research and Development of Photovoltaic Energy (IRDEP), UMR 7174 CNRS/EDF R&D/Chimie ParisTech-PSL, 6 quai Watier, 78401 Chatou, France
3 EDF R&D, Departement EFESE, 6 Quai Watier, 78401 Chatou, France
a
e-mail: julien.vidal@gmail.com
Received: 4 November 2016
Accepted: 13 June 2017
Published online: 1 August 2017
Formation entropy of point defects is one of the last crucial elements required to fully describe the temperature dependence of point defect formation. However, while many attempts have been made to compute them for very complicated systems, very few works have been carried out such as to assess the different effects of finite size effects and precision on such quantity. Large discrepancies can be found in the literature for a system as primitive as the silicon vacancy. In this work, we have proposed a systematic study of formation entropy for silicon vacancy in its 3 stable charge states: neutral, +2 and –2 for supercells with size not below 432 atoms. Rationalization of the formation entropy is presented, highlighting importance of finite size error and the difficulty to compute such quantities due to high numerical requirement. It is proposed that the direct calculation of formation entropy of VSi using first principles methods will be plagued by very high computational workload (or large numerical errors) and finite size dependent results.
© P. Seeberger and J. Vidal, published by EDP Sciences, 2017
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License
(http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License
(http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Formation free energies of point defects ΔGf are crucial quantities as they dictate for most part the temperature dependence of numerous macroscopic quantities such as diffusion coefficient [1] or carrier concentration [2]. In the case of photovoltaic applications, point defects play an important role either in setting the electrical properties of the different semiconductor layers forming photovoltaic devices or in affecting the recombination of the photogenerated charge carrier. For the last decades, much research has been dedicated to correctly describe the formation enthalpy ΔHf of isolated (the so-called dilute limit) point defects in multiple systems ranging from metals to semiconductors [3, 4, 5, 6]. While several robust formalisms have been established to compute such quantities, for example the supercell approach or the cluster approach, many challenges remain for years in order to obtain accurate values of formation enthalpies mainly because of finite size effects, the presence of long range electrostatic or elastic interactions [4, 7, 8, 9] and Density Functional Theory (DFT) deficiency to correctly describe band gaps [10]. Yet, the formation enthalpies of point defects are far from being sufficient to precisely describe the thermally activated formation of point defects occurring at relatively high temperature during synthesis. Thereby, temperature appears as a crucial parameter to include in atomistic calculation in order obtain deeper insights in the formation of point defects.
Regarding the temperature dependence of formation free energy, temperature effects have been routinely accounted for in (i) the chemical potentials of elements whose standard thermodynamical state is gaseous such as oxygen [11, 12], (ii) electronic formation entropy particularly in metallic state [13] or (iii) the configurational entropy term which allows one to calculate concentration of point defects from formation free energy. While less common than the calculations of formation enthalpies, the calculations of formation entropy ΔSf of point defects have become more and more popular in recent years and have already been carried out for variety of complex systems such as oxides [14], chalcogenides [15], semiconductors [16, 17], metals [18, 19], employing various techniques ranging from first principles including either Density Functional Perturbation Theory (DFPT) or Frozen Phonon (FP) [16, 17, 20, 21, 22] to Monte Carlo (MC) [23, 24] or Molecular Dynamics (MD) coupled with empirical potentials [25, 26]. Yet, it is rather difficult to adress the precision of such calculations and it has only been done on very specific systems such as aluminum or copper [27, 28] where very fine sampling of Brillouin zone coupled with accelerated convergence strategy such as thermodynamical integration were evidenced to be necessary to reach sufficient convergence below 1 meV/atom [27, 28]. Another important aspect of the calculation of formation entropy is the transition from large simulation box using simple interaction potential such as the popular Stillinger Weber potential for Si [29] to much smaller simulation box with the use of ab initio techniques. At first sight, such transition would appear to be beneficial to the accuracy and correctness of the calculation. However, it will be shown in this study that this is not automatically the case. Therefore, there is a clear need for deeper understanding of potentiel errors in the calculation of formation entropy and adressing the current available corrections based on elastic theory.
Two most important technicalities of the calculation is the definition of the simulation box including its boundary conditions and the type of Hamiltonian one has to solve. Such choice reflects on several important aspects of the formation entropy. A popular choice for the simulation box is the use of the supercell approach with periodic boundary conditions. In that case, strong finite size errors are expected, yet depending on the interaction at play (electrostatic, elastic, etc.) correction schemes can be derived to correct for such errors. Additionally, if one were to use a DFT Hamiltonian, the lack of a universal energy reference of DFT makes the calculation of formation enthalpy and entropy more difficult [4, 30]. In order to circumvent such problem, constant volume calculations are usually adviced. However, from a experimental point of view, the transition from constant volume to zero pressure quantities is much more desirable due to the difficulty to measure the constant volume ones. On the other hand, one of the most popular technique for defect calculation i.e. supercell approach intrinsically implies the use of a constant volume formalism mainly because of variation in basis set (the so-called Pulay stress) and loss of a common electrostatic reference [4]. While the former can be easily cured by an adequate choice of overconverged basis set, the latter remains problematic particularly in the case of semiconductor materials. Hence, the choice of a constant volume formalism appears to be both a necessity because of electrostatic effects and a shortcoming in terms of elastic finite size effect. Attempts to account for such transition has been proposed from an elastic theory point of view [8, 9, 31] mainly involving volume-based correction and from an anharmonic and quasiharmonic point of view [27].
 |
Fig. 1 Formation entropies for the Si vacancy from literature. References are with the first letter of the authors last names and the year the paper was published: SS0Y15 [21], MN03 [20], MB93 [23], CA93 [25], RF07 [31], DMK86 [32], BSCLAP93 [33], LA82 [34]. |
The silicon vacancy VSi represents a challenging system as its ground state local structure surrounding the defect is still under debate in the community [35, 35, 36, 37]. Both finite size effects and underestimation of band gap by DFT have been pointed out as responsible for the difficulty to stabilize some structural motives in simulation [38]. Thereby, either large supercells (beyond 216 atoms) or the use of hybrid functionals are usually required to stabilize the true ground state e.g. D2d symmetry in the neutral state ([8, 39]. Figure 1 shows the calculated vibrational formation entropies reported in the literature using different techniques and supercell sizes. Large discrepancies are observed considering either the general form of the vibrational formation entropy or its minimum (maximum) value at 1000 K being −4kB (11kB). Such differences cannot be assigned unambiguously to the many diverse technicalities of the calculation: supercell size (ranging from tenths of thousands to tenths of atoms), ensemble type considered (NVT versus NPT) for the dynamics, techniques used to compute the phonon spectrum (MD versus FP versus DFPT), restriction applied to phonon modes to be considered (local harmonics versus full harmonics), type of Hamiltonian considered (empirical potential versus ab initio), or the local symmetry of the silicon vacancy investigated (unrelaxed Td versus relaxed Td versus C2v versus D2d versus D3d). Experiments such as Electron Paramagnetic Resonance (EPR) have without a doubt shine light on the local symmetry of VSi evidencing the existence of a Jahn Teller relaxation and ruling out Td symmetry as the ground state structure [40]. Yet, the energetics of VSi is known indirectly via the experimental knowledge of silicon vacancy concentration at temperature closed to the melting point and the theoretical knowledge of the formation enthalpy ΔHf of VSi. However, several issues plague such indirect determination of the formation entropy: (i) formation enthalpy of VSi has been calculated to be over 3 eV resulting in very low concentration of defects (typically in the range of 1015 or 1016cm-3) at temperature close to the melting point, (ii) large discrepancies in the calculated values of ΔHf in particular depending on the functional used [36]: a 0.5 eV change in ΔHf results in a change of formation entropy of nearly 4 kB at temperature close to the melting point, (iii) existence of other types of formation entropy playing a significant role at high temperature such as entropy of ionization or entropy of electronic excitation [41], (iv) large discrepancies in the value of the configuration entropy ranging from 1.1 kB[33] to 7kB[25] and finally (v) difficulty to clearly decipher experimentally between single vacancies and extended vacancies or amorphous nanodomains.
In this paper, the calculation of the formation entropy of silicon vacancy has been performed using the simple frozen phonon approach and focusing mainly on some methodological aspects of the calculation particularly the supercell size and then investigating the formation entropy of VSi for different charged states. The choice of the methods is particularly critical as the system size increase. DFPT technique is the ultimate way to calculate phonon properties as it does not depend on any parameter while in the case of frozen phonon, magnitude of displacement has to be set and is critical so as to increase the precision of the calculations. Baroni et al. proposes a scaling for the computational workload of both frozen phonon and DFPT [42]. DFPT is clearly advantageous when dealing with high symmetry system with little number of atoms. However, in the case of a supercell with a defect, one could consider that the supercell is in part the reflection of the Si primitive cell but also the primitive cell of the system VSi:Si. Consequently, the number of unequivalent atom Nat can be considered equal to the number of atoms in the supercell Nsc and the Brillouin zone shrinks to a very small volume. In that case, DFPT and frozen phonon approach (assuming a scaling of  for DFT) are found to be equivalent in terms of scaling
for DFT) are found to be equivalent in terms of scaling  .
.
2 Technical details
Calculations were performed using the VASP [43] package within the Projected Augmented Wave formalism (PAW) [44]. The phonon spectrum was calculated within the frozen phonon approximation using PHON code [45] and making use of the supercell to infinite lattice transformation. Supercell sizes ranging from 54 atoms to 432 atoms have been investigated. A cut-off energy of 500 eV was used together with a 12 × 12 × 12 k-point grid for the 2-atom primitive cell. During the relaxation stage, no symmetry was imposed to the system. On the other hand, during the generation of the non equivalent displacements necessary to construct the interatomic force constant matrix within the frozen phonon formalism, the symmetry of the system was redetermined and subsequently used to reduce the number of displacements generated and improve the accuracy of the calculation through a subsequent symmetrization of the interatomic force constant. Because of the latter, special attention should be drawn to the correct convergence of the density of states with respect to q-point. In addition, particular care has been taken to deal with (i) real space projection and Fast Fourier Transform, (ii) sufficient minimization of the forces acting on each atom to obtain the equilibrium crystal structure, (iii) magnitude of the displacement and (iv) energy cutoff for the augmentation sphere leading to an improved precision with a moderate increase in computational workload, (v) central difference scheme to determine the interatomic force constant, (vi) fine sampling of the frequency domain and improved numerical scheme for DOS integration. The Generalized Gradient Approximation (GGA) [46] has been used as it was shown to be less prone to negative modes in the case of the silicon vacancy [20]. In order to compute thermodynamical quantities, phonon calculations have been extrapolated to a 40 × 40 × 40 q-point grid for the defective supercell and a 100 × 100 × 100 q-point grid for the perfect one with a gaussian smearing of 0.02 THz for both. Throughout the paper, thermodynamical quantities were calculated either at constant volume i.e. all internal relaxations were performed at fixed lattice constant obtained with GGA functionals (5.403Å and 5.465 Å respectively) in good agreement with experiment(a = 5.431 Å [47]) or at zero pressure. The effect of the former formalism can be monitored through the hydrostatic external pressure acting on the supercell as a consequence of the presence of a vacancy in the crystal. In the case of the 432 atom supercell, external pressures of –2.35 kB, 0.54 kB and –4.3 kB have been calculated for neutral defect in D2d configuration, charged defect q = −2 in D3d configuration and q = −2 in Td configuration respectively. Internal relaxation have been carefully monitored as the VSi systems has been shown to be cumbersome to deal with in terms of force minization [48]: a combination of conjugate gradient and quasi Newton algorithm has been employed in order to achieve below 5 × 10-5eV/Å precision for forces acting on each atom. It was found that for supercell with number of atoms below 432, internal coordinates were difficult to relax because of the large hydrostatic external pressure acting on the supercell with the notable exception of the Td symmetry in the neutral charge state.
Found stable defect structures of the neutral and charged silicon vacancy are displayed. Found ground state structures within this study are marked with a bullet • and other authors are referenced. Symmetry-labels are given in Schnflies notation and distances R between the ions neighbouring the vacancy for the 432 atom cell are given in Å. Furthermore total energies Etot, energy differences ΔE and for the neutral vacancy the formation enthalpies ΔHf are displayed.
3 Ground state structure
Table 1 displays the energetics of the different symmetries as a function of the charge states of the silicon vacancy. As mentioned in the introduction, due to finite size errors, a supercell of 432-atom has been employed to relax the structure and obtain the total energies. It was found that the correct description of the ground state of the neutral vacancy is possible with supercell size down to 216-atom in agreement with previous reports [36, 38]. For local symmetries significantly differing from the Td structure, it was required to perform an initial random displacement of the first neighbour atoms, so the minization algorithm is able to escape the Td-symmetry configuration. For the neutral defect, the D2d structure was found to be located at approximatively 0.2 eV lower in energy than the Td structure, demonstrating a Jahn-Teller distortion. For charge state +2, the energy of the Td structure is 0.15 eV lower than the one of D2d while for the −2 charge state, a split vacancy with D3d symmetry is 0.2 eV more stable compared to the second lowest energy structure, C2v. All the ground state structures found for charge states 0, +2 and –2 are in agreement with previous theoretical studies [35, 36, 37, 38, 49] and with DLTS and EPR studies of Watkins [40, 50]. As Table 1 shows, the main discrepancies between previously published results occur for the defect charge states +1 and –1. However, such defect states are found not to be stable within the range of chemical potential defined by the Si band gap [36], leading to a negative-U behavior for both negatively and positively charged states.
The interatomic distances between the atoms define precisely the local symmetry of the defect. Changes in atomic distances between two different arrangements are found to be much larger than the atomic displacement used in the FP approach preventing the exploration of multiple potential well during the phonon calculation. Additionnally, we performed Climbing Image Nudged Elastic Band (CI-NEB) [51] with reduced cutoff and k-point grid (namely a 400 eV cutoff energy for the plane wave basis set and Γ-only k-point grid) in order to determine the presence of an energy barrier between the different configurations for a given charge state. First, it is worth mentioning that while the hierarchy of the different local configurations is preserved under the relaxed convergence criteria, the magnitude of the energy difference between them is impacted by the low precision settings as one can see comparing Figure 2 and Table 1. This shows again that simple technicalities (type of pseudopotentials, cutoff energies, k-point grid or size of the supercell) can affect considerably the potential energy surface of VSi system, which has been already discussed in previous works [31, 38, 52]. In all cases, it was found that the local rearrangements of the four first neighbour atoms differing from the ground state one are metastable configurations i.e. involving negative vibrational modes. In the case of the neutral defect and Td arrangement, phonon calculations have been performed and a significant number of negative eigenvalues of the Hessian matrix (up to 0.2% in the case of the 40 × 40 × 40q-point grid) were obtained from diagonalization of the interatomic force constant matrix. As it will be shown in the next section, the existence of negative eigenvalues evidently complicates a precise estimation of the low energy phonon density of states, which is the main ingredient of the vibrational formation entropy. Moreover, the inclusion of soft or negative phonon modes would mean that anharmonic terms has to be accounted for as high order elastic constant terms may dominate over the quadratic ones [53]. Van Vechten estimated an upper bound for the formation entropy related to the softening of a single mode within the harmonic approximation ΔSf ≈ 3kB. Second order anharmonic terms were found to contribute negatively to the formation entropy when restricting the energy expansion to 4th order terms. It is still unclear how higher order terms will contribute to the formation entropy though [53]. It is then clear that the use of unrelaxed structure or the metastable local arrangement must be avoided.
 |
Fig. 2 Energy profile between different local arrangements of the 1st neighbour atoms surrounding the silicon vacancy. |
4 Vibrational formation entropy
The vibrational formation entropy for the silicon vacancy is given by the compact expression  (1)where N is the number of atoms considered in the supercell, Sdefect is the vibrational entropy of the supercell containing a vacancy and Shost is the vibrational entropy of bulk silicon. One should notice that the factor N−1 /N accounts for the temperature dependance of the elemental chemical potential of Si. Such formula involving integrated quantities is in practice used to compute
(1)where N is the number of atoms considered in the supercell, Sdefect is the vibrational entropy of the supercell containing a vacancy and Shost is the vibrational entropy of bulk silicon. One should notice that the factor N−1 /N accounts for the temperature dependance of the elemental chemical potential of Si. Such formula involving integrated quantities is in practice used to compute  , giving little insight in the different frequency contributions. However, the formation entropy of a defect can be recast as a frequency integration such as [55]
, giving little insight in the different frequency contributions. However, the formation entropy of a defect can be recast as a frequency integration such as [55]  (2)where n is the Bose-Einstein distribution and Δgnorm(ω) the normalized difference of phonon density of states (DOS) between the defective and host supercell. From equation (2), one should notice that the formation entropy is proportional to N × Δgnorm, meaning that if one were to reach the dilute limit by increasing the size of the supercell i.e. N, Δgnorm should become increasingly smaller so that
(2)where n is the Bose-Einstein distribution and Δgnorm(ω) the normalized difference of phonon density of states (DOS) between the defective and host supercell. From equation (2), one should notice that the formation entropy is proportional to N × Δgnorm, meaning that if one were to reach the dilute limit by increasing the size of the supercell i.e. N, Δgnorm should become increasingly smaller so that  converges towards a finite value. Such drastic requirement on the phonon density of states has already been necessary for the calculation of integrated quantities such as non radiative capture cross section [22]. Moreover, because of the peculiar feature of the weighting function in equation (2), low energy acoustic modes will contribute significantly more to the formation entropy than high energy optical modes, particularly at low temperature (see Fig. 3). In the context of metastable configuration described in the previous section, large errors may stems from the low energy modes giving rise to a positive contribution to the formation entropy. Therefore, the use of the correct ground state structure is strongly advised when considering the calculation of the formation entropy of a point defect particularly when employing the FP method with finite displacements. Finally, one should also notice that equation (2) is an unusual expression of the formation entropy: formation entropy formula is commonly discretized i.e. the summation is realized over all the phonon modes of the supercell i.e. 3N in the case of the host supercell and 3(N−1) in the case of the vacancy supercell. The q-point dependency of the expression while not obvious at first sight, is included in the 3N modes of the host supercell and vacancy supercell. As it will be shown in the next section, such expression hides in part the strong cross cancellation of different frequency regions when such such frequency regions are reachable in terms of the q-point sampling implied by the choice of the supercell.
converges towards a finite value. Such drastic requirement on the phonon density of states has already been necessary for the calculation of integrated quantities such as non radiative capture cross section [22]. Moreover, because of the peculiar feature of the weighting function in equation (2), low energy acoustic modes will contribute significantly more to the formation entropy than high energy optical modes, particularly at low temperature (see Fig. 3). In the context of metastable configuration described in the previous section, large errors may stems from the low energy modes giving rise to a positive contribution to the formation entropy. Therefore, the use of the correct ground state structure is strongly advised when considering the calculation of the formation entropy of a point defect particularly when employing the FP method with finite displacements. Finally, one should also notice that equation (2) is an unusual expression of the formation entropy: formation entropy formula is commonly discretized i.e. the summation is realized over all the phonon modes of the supercell i.e. 3N in the case of the host supercell and 3(N−1) in the case of the vacancy supercell. The q-point dependency of the expression while not obvious at first sight, is included in the 3N modes of the host supercell and vacancy supercell. As it will be shown in the next section, such expression hides in part the strong cross cancellation of different frequency regions when such such frequency regions are reachable in terms of the q-point sampling implied by the choice of the supercell.
 |
Fig. 3 Integration function (n + 1)ln(n + 1)−nln(n) of equation (2) as a function of frequency for different temperature values. |
 |
Fig. 4 Phonon density of states of Si obtained from the FP approach for different sizes of supercell calculated using the GGA functional. Experimental data are taken from reference [56]. |
 |
Fig. 5 Vibrational entropy of Si obtained from the FP approach for different sizes of supercell. Experimental data are taken from reference [56]. |
As an example, Figure 4 shows the phonon density of states calculated for bulk Si considering different supercell size corresponding to different sampling of the reciprocal space in the case of the FP approach. In this figure, the gaussian smearing used to generate the DOS was fixed while the q-point grid was refined until the convergence of the density of states was reached. It was found that a 100 × 100 × 100q-point grid is necessary to obtain a smooth spectrum. Indeed, it was particularly difficult to converge low density regions namely between 0 and 2 THz and between 6 and 8 THz where highly degenerate modes occur. In Figure 4, significant convergence of the density of states is obtained for supercells larger than 432 atoms, which translates into a minimum 6 × 6 × 6q-point sampling for the construction of the dynamical matrix. One should notice however that small differences persist mainly in the TA, TA’ and TO/LO region. In order to assess the convergence of the density of states with respect to thermodynamical quantities of interest, the vibrational entropy of Si has been subsequently estimated from the phonon density of states shown in Figure 4: very good agreement with experiments is observed and fast convergence of vibrational entropy is also observed with 128 atom supercell displaying a 0.01 kB/atom error over the whole range of temperatures. Therefore it seems that the choice of a 432 atom supercell will ensure a sufficiently precise estimation of the bulk formation entropy. Further considerations related to the defect formation entropy such as difficulty to retain sufficient numerical precision when increasing the size of the supercell, difficulty to stabilize the ground state local structure of defects or necessary accomodation of the strain field created by the vacancy [21, 35, 48] confirm the relevance of such a choice. A frequency decomposition of the ΔS = S432−S1458 has been performed over 6 different frequency regions that will be defined later on for the analysis of the defect formation entropy: Figure 6 indicates that the total error on the vibrational entropy of a 432 atom supercell is less than 1 kB, yet the frequency decomposition reveals a strong cross cancellation between different frequency ranges with the largest error made on the low density region TA Part 1 and TA’ Part 3, where a small decrease of the phonon DOS can be observed visually (see the black arrow in Fig. 1). Therefore, it seems obvious that one has to use a bulk vibrational entropy commensurate to the defect supercell employed i.e. either with a commensurate q-point grid in the case of DFPT or the same size of supercell in the case of FP formalism.
 |
Fig. 6 Difference of vibrational entropy for 432 atom perfect supercell considering the normalized phonon DOS obtained from a 432 atom supercell and a 1428 atom supercell. |
The choice of the gaussian smearing is also of critical importance. Artificial smearing has been particularly useful in improving accuracies of integrated quantities, making the choices of the smearing and q-point sampling particularly intricated though. On the other hand, smearing carries also a physical meaning as phonon lifetime originating from phonon-phonon interactions [57, 58]. The lifetime of a phonon state is also highly dependent on the nature of the state and its nominal frequencies, with high lifetime found for low frequency acoustic modes (τ ≈ 10ns corresponding to a smearing of 10-4THz)and low lifetime for high frequency optical modes (τ ≈ 2ps corresponding to a smearing of 0.5 THz) [59]. Therefore, the value of smearing chosen for this study i.e. 0.05 THz seems to be a relatively good compromise. Increase of the gaussian smearing from 0.05 THz to 0.1 THz was found not to modify the value of the formation entropy while further increase to 0.5 THz induces change in the formation entropy of several kB. One should also notice that molecular dynamics approach will account automatically for phonon-phonon interaction beyond the harmonic approximation. In the context of a defective cell, a natural smearing due to the symmetry lowering induced by the presence of the vacancy occurs and is hardly quantifyable. As a consequence, phonon DOS of defective cells are much faster converging quantity than the phonon DOS of crystalline Si, with typically convergence obtained for q-point sampling as low as 50 × 50 × 50 for the 432 atom supercell.
Several correction schemes have been proposed to account for finite size error in the calculation of formation entropy. Most of the corrections are based on quite drastic assumptions such as the spherical symmetry of the defect cluster or isotropy of the formation volume [19, 31, 60]. Surprisingly, in some cases, if one were to consider a direct approach to the finite size issue, i.e. increase the size of the simulation box, formation entropy was found to diverge [31, 60]. Therefore, an embbedded cluster approach has been proposed early on such as the simulation box is partitioned into two regions: a defect or core region where the vibrational spectrum is treated exactly i.e. solving the force constant matrix for the phonon frequencies surrounded by an elastic region where the entropy is derived from the elastic strain. Still, the correction proposed for the embedded cluster approach presents some divergence when the size of the defect region is extended to the boundary of the simulation box [31]. In the case of a supercell approach under constant volume constraint and the size of the supercell sufficiently large with respect to the size of the core regions, Mishin et al. devised a straightforward elastic correction ΔSel at first order in N (total number of atoms) and nc (total number of atoms in the core region) [19];  (3)where ν is Poisson ratio, α the thermal expansion coefficient, B the bulk modulus and vrel the defect relaxation volume in an infinitely large volume. The latter corresponds to the dilatation part of the volume increase or decrease of the core region and per se is also dependent on its arbitrary definition. Rauls et al. considered a core region of 17 atoms corresponding to the first and second shell neighbour and subsequently calculated vrel of –20 Å3 for a 256-atom supercell. If one were to consider equation (3) with experimental values for ν, α and B, the elastic correction would then be 0.2 kB. On the other hand, similar corrections derived from reference [31], one would obtain a correction linearly dependent on the number of atoms in the supercell which compensates the divergence of the uncorrected ΔSf. Finally, following the argument of volume change, Fernandez et al. proposed an elastic correction such as
(3)where ν is Poisson ratio, α the thermal expansion coefficient, B the bulk modulus and vrel the defect relaxation volume in an infinitely large volume. The latter corresponds to the dilatation part of the volume increase or decrease of the core region and per se is also dependent on its arbitrary definition. Rauls et al. considered a core region of 17 atoms corresponding to the first and second shell neighbour and subsequently calculated vrel of –20 Å3 for a 256-atom supercell. If one were to consider equation (3) with experimental values for ν, α and B, the elastic correction would then be 0.2 kB. On the other hand, similar corrections derived from reference [31], one would obtain a correction linearly dependent on the number of atoms in the supercell which compensates the divergence of the uncorrected ΔSf. Finally, following the argument of volume change, Fernandez et al. proposed an elastic correction such as  (4)where γ is the thermal Gruneïsen parameter and vSi is the equilibrium atomic volume, which would yield a correction of 1.2 kB/atom (with the correction restricted to core atom) if one were to consider vrel = −20Å3 and γ from [56]. The relaxation volume vrel defined in equations (3) and (4) may differ from the relaxation volume derived from the thermodynamical formation volume
(4)where γ is the thermal Gruneïsen parameter and vSi is the equilibrium atomic volume, which would yield a correction of 1.2 kB/atom (with the correction restricted to core atom) if one were to consider vrel = −20Å3 and γ from [56]. The relaxation volume vrel defined in equations (3) and (4) may differ from the relaxation volume derived from the thermodynamical formation volume  . The former relaxation volume calculated as the change in total volume of the defect supercell is –24.1 Å3 in good agreement with previous calculation [61, 62]. The relaxation volume varies only marginally in the range of supercell size considered in this study: from –22.8 Å3 for the 216-atom supercell to –25.5 Å3 for the 1024 atom supercell, yielding a limit for N → ∞ of –26.3 Å3. On the other hand, the term vrel of equations (3) and (4) is defined as a function of the size of the core region. Following reference [31], we consider all second neighbour atoms and computed the displacement of the atoms u with respect to second neighbour distance in a perfect crystal in the case of constant volume and zero pressure calculation. The displacements were found to be similar in either cases but in both cases to display a high anisotropy as four out of twelve second neighbour atoms display a displacement –0.27 to –0.3 Å while all other second neighbour atoms were hardly displaced (i.e. u ≈ −0.01Å), thus violating the spherical symmetry approximation of reference [20]. Nevertheless, as a very rough approximation, one can estimate the relaxation volume as defined in reference [19] and equation (3) to be –28 Å3, which considering the strong anisotropy of u is in fairly good agreement with the value of vrel obtained in reference [31]. Finally, Rauls et al. obtained an elastic correction derived from the one proposed by Mishin [19], yielding a rather large correction of 6.1 kB in the case of VSi in the D2d configuration. In the case of charged defects, the correction might be significantly different as the relaxation volumes are drastically different: the relaxation volume
. The former relaxation volume calculated as the change in total volume of the defect supercell is –24.1 Å3 in good agreement with previous calculation [61, 62]. The relaxation volume varies only marginally in the range of supercell size considered in this study: from –22.8 Å3 for the 216-atom supercell to –25.5 Å3 for the 1024 atom supercell, yielding a limit for N → ∞ of –26.3 Å3. On the other hand, the term vrel of equations (3) and (4) is defined as a function of the size of the core region. Following reference [31], we consider all second neighbour atoms and computed the displacement of the atoms u with respect to second neighbour distance in a perfect crystal in the case of constant volume and zero pressure calculation. The displacements were found to be similar in either cases but in both cases to display a high anisotropy as four out of twelve second neighbour atoms display a displacement –0.27 to –0.3 Å while all other second neighbour atoms were hardly displaced (i.e. u ≈ −0.01Å), thus violating the spherical symmetry approximation of reference [20]. Nevertheless, as a very rough approximation, one can estimate the relaxation volume as defined in reference [19] and equation (3) to be –28 Å3, which considering the strong anisotropy of u is in fairly good agreement with the value of vrel obtained in reference [31]. Finally, Rauls et al. obtained an elastic correction derived from the one proposed by Mishin [19], yielding a rather large correction of 6.1 kB in the case of VSi in the D2d configuration. In the case of charged defects, the correction might be significantly different as the relaxation volumes are drastically different: the relaxation volume  is calculated at 5.4 Å3 and –44.4 Å3 for –2 charge state in the D3d and +2 charge state in the Td configuration respectively in agreement with the hydrostatic external pressure introduced previously. Interestingly, the displacement u of the second shell atoms are considerably different in both cases: for Td symmetry and charge state +2, no noticable displacement is observed except for 3 atoms with displacement u of –0.06 Å while for D3d symmetry and charge state –2, 6 atoms out of 12 are displaced by –0.26 Å. Therefore, one can clearly foresee that the entropy stored in the domain comprised between the core region and the boundaries of the simulation box is much more important in the case of charge states –2 than +2.
is calculated at 5.4 Å3 and –44.4 Å3 for –2 charge state in the D3d and +2 charge state in the Td configuration respectively in agreement with the hydrostatic external pressure introduced previously. Interestingly, the displacement u of the second shell atoms are considerably different in both cases: for Td symmetry and charge state +2, no noticable displacement is observed except for 3 atoms with displacement u of –0.06 Å while for D3d symmetry and charge state –2, 6 atoms out of 12 are displaced by –0.26 Å. Therefore, one can clearly foresee that the entropy stored in the domain comprised between the core region and the boundaries of the simulation box is much more important in the case of charge states –2 than +2.
 |
Fig. 7 DOS difference Δg(ω) for neutral defect VSi in the D2d configuration. Black broken line represent the fitting function in the low frequency range. |
5 Neutral vacancy in the D2d configuration
Figure 7 shows the values of Δg(ω) for the neutral charge state in the D2d configuration for a 432-atom supercell. The frequency space have been divided into 7 regions according to values of Δg(ω), the type of phonon mode and features of the crystalline silicon phonon DOS as seen in Figure 4: 3 frequency ranges for the transverse acoustic (TA) modes corresponding to the low DOS region [0, 3.6 THz] (TA Part 1), the TA peak region [3.6, 5.4 THz](TA Part 2), the TA’ peak region [5.4, 6.8 THz] (TA Part 3), 2 frequency ranges for the longitudinal acoustic modes (LA) a low DOS region [6.8, 9 THz] (LA Part 1) and one corresponding to the longitudinal acoustic peak LA region [9, 11 THz] (LA Part 2), one corresponding to the broad LO/LA peak [11, 13 THz] (LO/LA) and finally one corresponding to the TO/LO peak region [13–16 THz]. From the point of view of the Brillouin zone sampling, the acoustic peak regions corresponds to phonon vibrations flattening out when approaching the irreducible Brillouin zone vertices. In the embedded cluster framework, the limitation of the dynamical region to a small volume centered at the vacancy location involves that the q-point sampling of the IBZ is limited to certain region, probably Γ and IBZ boundaries. Overall, the differences Δgnorm(ω) between the two normalized phonon densities of states are extremely small with typical values around 10-3THz-1 and maximum values occuring for the LO/LA and TO/LO modes in the high frequency regions. This appears to be in contradiction with previous studies where difference in phonon DOS densities were much more pronounced over the full frequency range [20, 25]. The main feature of Δgnorm(ω) is the softening of the optical modes, which can be viewed as a succession of positive and negative Δgnorm in Figure 7 in agreement with previous calculations [20]. On the other hand, while quite small, a systematic softening of the transverse acoustic modes also occurs as evidenced by the increase in phonon DOS in the TA Part 1 region. Interestingly, the phonon modes originating from this region are characterized by very low values of q-vector corresponding to long range distortion of the lattice. Therefore, it is commonly considered as one of the most difficult region to model as very large supercells must be employed in order to sample efficiently the Brillouin zone next to q = 0. In the case described in this study, the typical sizes of supercell used for phonon calculation only allow to directly probe frequency region down to 2–3 THz: yet, interpolation scheme is used to obtain accurate density of states even at low frequency [45]. In order to estimate the error made with such procedure, the frequency integration over TA Part 1 has been parted down such as to obtain constant 1 kB contribution: it is noticed that the region between 0 THz ad 1.75 THz only contributes 1 kB to the total  . Incidently, the long range distortion associated with acoustic waves originating from the low frequency region of the phonon DOS also corresponds to the elastic correction stored in the region delimited by the defect core and the simulation box boundaries as described in the previous section (see Eqs. (3) and (4)). The behavior of Δgnorm(ω) in this range of frequency can be described quite effectively considering a change in sound velocity induced by the defect such as
. Incidently, the long range distortion associated with acoustic waves originating from the low frequency region of the phonon DOS also corresponds to the elastic correction stored in the region delimited by the defect core and the simulation box boundaries as described in the previous section (see Eqs. (3) and (4)). The behavior of Δgnorm(ω) in this range of frequency can be described quite effectively considering a change in sound velocity induced by the defect such as  (5)where V0 is the volume of the unit cell, c′ is the speed of sound for the defective cell and c is the speed of sound for the perfect cell. The function corresponding to equation (5) has been fitted between 0 and 3 THz and yield a reduction of c′ of 2.7%. One should also notice that the precise estimation of c is a particularly intensive computational task, mainly due to the very small energy difference at play in this frequency region and the requirement for very high numerical precision [63, 64]. Moreover, some of the previously reported formation entropy calculations have been performed for q = 0 only and for small supercell size, resulting in a featureless DOS in the low frequency range [15, 25]. Such approach, while inaccurate at first sight, might be a good comprise if one were to avoid the hurdle to improve numerical accuracy while increasing the supercell size. Besides, it might also prevent double counting when considering elastic correction. Ackland et al. reported the variation of elastic constant as a function of the defect concentration: the so-called defect strain polarizabilities αij[25]. VSi is found to be an important stiffening agent compared to other point defects such as self interstitials. In the most simple case, i.e. ct,l, [100] and cl, [111], it was found moderate changes of the speed of sound due to the presence of a defect of +0.7%, –0.3% and 0.4% respectively, much smaller than the 2.7% reduction found through the fitting procedure. Finally, one can also assert the change in speed of sound due to the change in volume by considering the Grüneisen parameter of LA and TA modes γLA,TA which is strictly positive with an average value of 0.5 and typical values of vrel ≈ −20Å3. Upon volume change, the phonon frequency for LA and TA modes are very slightly downshifted resulting in a decrease of c by less than 1% in agreement with the observed softening of the acoustic modes and decrease of the speed of sound. The observed discrepancies between the direct analysis of Δg(ω) and the elastic constant analysis can be attributed to (i) numerical error in estimating both speed of sound and defect strain polarizabilities [64], (ii) the difficulty to correctly describe this frequency region due to use of FP approach for a system with relatively flat energy landscape [61], (iii) volume effect are also known to influence the phonon vibration spectrum [20].
(5)where V0 is the volume of the unit cell, c′ is the speed of sound for the defective cell and c is the speed of sound for the perfect cell. The function corresponding to equation (5) has been fitted between 0 and 3 THz and yield a reduction of c′ of 2.7%. One should also notice that the precise estimation of c is a particularly intensive computational task, mainly due to the very small energy difference at play in this frequency region and the requirement for very high numerical precision [63, 64]. Moreover, some of the previously reported formation entropy calculations have been performed for q = 0 only and for small supercell size, resulting in a featureless DOS in the low frequency range [15, 25]. Such approach, while inaccurate at first sight, might be a good comprise if one were to avoid the hurdle to improve numerical accuracy while increasing the supercell size. Besides, it might also prevent double counting when considering elastic correction. Ackland et al. reported the variation of elastic constant as a function of the defect concentration: the so-called defect strain polarizabilities αij[25]. VSi is found to be an important stiffening agent compared to other point defects such as self interstitials. In the most simple case, i.e. ct,l, [100] and cl, [111], it was found moderate changes of the speed of sound due to the presence of a defect of +0.7%, –0.3% and 0.4% respectively, much smaller than the 2.7% reduction found through the fitting procedure. Finally, one can also assert the change in speed of sound due to the change in volume by considering the Grüneisen parameter of LA and TA modes γLA,TA which is strictly positive with an average value of 0.5 and typical values of vrel ≈ −20Å3. Upon volume change, the phonon frequency for LA and TA modes are very slightly downshifted resulting in a decrease of c by less than 1% in agreement with the observed softening of the acoustic modes and decrease of the speed of sound. The observed discrepancies between the direct analysis of Δg(ω) and the elastic constant analysis can be attributed to (i) numerical error in estimating both speed of sound and defect strain polarizabilities [64], (ii) the difficulty to correctly describe this frequency region due to use of FP approach for a system with relatively flat energy landscape [61], (iii) volume effect are also known to influence the phonon vibration spectrum [20].
 |
Fig. 8 Frequency contribution to the vibrational formation entropy |
Figure 8 shows the evolution of  as a function of T for the neutral silicon vacancy in the D2d configuration together with the entropic contribution from the different frequency regions defined previously. The total vibration formation entropy is the result of strong cross-cancellation of contributions originating from different frequency regions, with a high temperature value of 8.3 kB. The softening of the optical modes results in a large positive contribution (up to 20 eV in absolute value) originating from the LO/LA region and a large negative contribution from the TO/LO region. Despite their quite large absolute value, the softening of optical modes results in an overall negative contribution of –3.6 kB to the total formation entropy. The second main contributions originate from low density of states region namely TA Part 1 and LA Part 1. As discussed previously such frequency region are rather difficult to sample due to their restriction to small zone of the IBZ and thus are more prone to computational error. Despite very low values of Δgnorm(ω) in the TA Part 1 frequency range, the integration function (n + 1)ln(n + 1)−nln(n) is maximum in this region and for low temperature, even several orders of magnitude higher than in frequency ranges corresponding to large values of Δgnorm(ω). Overall, TA Part 1 dominates the total formation entropy of D2d neutral VSi. One should notice that
as a function of T for the neutral silicon vacancy in the D2d configuration together with the entropic contribution from the different frequency regions defined previously. The total vibration formation entropy is the result of strong cross-cancellation of contributions originating from different frequency regions, with a high temperature value of 8.3 kB. The softening of the optical modes results in a large positive contribution (up to 20 eV in absolute value) originating from the LO/LA region and a large negative contribution from the TO/LO region. Despite their quite large absolute value, the softening of optical modes results in an overall negative contribution of –3.6 kB to the total formation entropy. The second main contributions originate from low density of states region namely TA Part 1 and LA Part 1. As discussed previously such frequency region are rather difficult to sample due to their restriction to small zone of the IBZ and thus are more prone to computational error. Despite very low values of Δgnorm(ω) in the TA Part 1 frequency range, the integration function (n + 1)ln(n + 1)−nln(n) is maximum in this region and for low temperature, even several orders of magnitude higher than in frequency ranges corresponding to large values of Δgnorm(ω). Overall, TA Part 1 dominates the total formation entropy of D2d neutral VSi. One should notice that  calculated in references [20, 21] displays the same temperature dependence and order of magnetiude as the formation entropy calculated in this study.
calculated in references [20, 21] displays the same temperature dependence and order of magnetiude as the formation entropy calculated in this study.
 |
Fig. 9 Phonon density of states for neutral defect VSi in the Td configuration. The grey filled curve represents the density of states of the perfect lattice for a 1428 atom supercell. |
 |
Fig. 10 High temperature frequency contribution to the vibrational formation entropy |
6 Finite size effects
The study of finite size effects in the case of VSi is complicated by the fact that the stable local configuration is dependent on the size of the supercell [38]. Despite the presence of negative phonon modes and for the sake of illustration, the Td configuration of VSi has been considered at first. In the cases of very small defect supercells, larger supercells have been constructed for the phonon calculation such as to properly sample the irreducible Brillouin zone. As previously discussed, Td configuration of the silicon vacancy is only stable for small supercell size: in the case of the 54 atom supercell, no negative modes were detected in the calculation, starting with the 128 atom supercell, the number of negative modes steadily increases from 5 × 10-4% to 0.15% for the 432 atom supercell and 0.06% for the 1024-atom supercell. Figure 9 shows the phonon density of states for different size of defect supercell containing a single silicon vacancy in the Td local configuration. Overall, it appears that convergence of the phonon density of states occurs over the full range of frequency with the deviation from the perfect phonon density of states becoming smaller and smaller. For the 1024 atom supercell, only sizable differences are observed in the LA/LO and TO/LO regions. The result obtained for the smallest supercell (e.g. 54 atom supercell) agrees with the one reported in the literature and obtained from DFPT [20], featuring an overall softening of the modes including the optical ones. The vibrational formation entropy has been estimated subsequently using the 432 atom and 1024 atom perfect supercell results for 54 and 432 atom defect supercell and 128 and 1024 atom defect supercell respectively (see Fig. 10). First, independently on the supercell size, the total vibrational formation entropy converges towards large positive values between 8 and 10 kB in agreement with previously published results [20]. Such trend is mainly driven by the large contribution originating from the low frequency region TA Part 1, which contributes 15 kB to the overall formation entropy. Moreover, it also appears that the high temperature formation entropy converges to two different values depending on the size of the supercell used to perform the phonon calculations: 8.5 kB for the 432 atom supercell for the 54 and 432 atom defect supercell and 10.2 kB for the 1024 atom supercell for the 128 and 1024 atom defect supercell. Similarly some parts of the frequency range contributions (TA Part 1, TA Part 2, TA’ Part 3) show very similar behavior: such frequency regions were already found to be extremely sensitive to the size of the supercell used to compute the phonon spectrum. On the other hand, the difference between the LA/LO and the TO/LO contributions seems to converge to a value of 1.5 kB. Finally, it is also interesting to notice that while the perturbation to the phonon density of states in the case of a 54 atom supercell seems to be extremely important, the final vibrational contribution is very close to the value obtained for the largest supercell used in this study i.e. 1024 atoms: to some extent, the N−1 factor in equation (2) is instrumental to the observed changes of vibrational formation entropy as a function of the supercell size. For small N, large perturbations at low frequency tend to be damped while for large N, small deviations in the same frequency region tend to be emphasized.
 |
Fig. 11 Phonon density of states for different charge of the defect VSi in their ground state configuration. The grey filled curve represents the density of states of the perfect lattice for a 432 atom supercell. Inset shows the vibrational formation entropy for the different charge states. |
 |
Fig. 12 Frequency contribution to the vibrational formation entropy |
 |
Fig. 13 Frequency contribution to the vibrational formation entropy |
7 Formation entropy of charged defects
The vibrational formation entropy of different charge states of VSi has also been investigated and the phonon density of states obtained for the different charge states in their respective ground state configuration is shown in Figure 11. All charge states display a significant transfert of phonon DOS from the TO/LO peak to the LA/LO region, resulting in a negative contribution to the total vibrational entropy. The total vibrational formation entropies 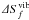 is very similar for all charge states (see inset of Fig. 11) including its shape and its high temperature asymptotic value. Yet, some of the frequency contributions to
is very similar for all charge states (see inset of Fig. 11) including its shape and its high temperature asymptotic value. Yet, some of the frequency contributions to 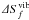 differ significantly as a function of the charge state. Figures 12 and 13 show the frequency decomposition of the total formation entropy for charge state +2 and −2, respectively. Compared to the frequency decomposition of
differ significantly as a function of the charge state. Figures 12 and 13 show the frequency decomposition of the total formation entropy for charge state +2 and −2, respectively. Compared to the frequency decomposition of 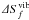 of the neutral charge state (see Fig. 8), charge state +2 displays a much larger contribution from TA Part 1 compensated by a negative contribution from TA’ Part 3 while contribution from LA Part 1 is significantly reduced. While
of the neutral charge state (see Fig. 8), charge state +2 displays a much larger contribution from TA Part 1 compensated by a negative contribution from TA’ Part 3 while contribution from LA Part 1 is significantly reduced. While  and
and  are reduced in absolute values, their difference
are reduced in absolute values, their difference  is found to be 1 kB higher than the value obtained for the neutral charge state. In the case of the –2 charge state with local symmetry D3d, such difference is rather large with value of –2.5 kB with absolute values of
is found to be 1 kB higher than the value obtained for the neutral charge state. In the case of the –2 charge state with local symmetry D3d, such difference is rather large with value of –2.5 kB with absolute values of  and
and  largely exceeding the one of neutral –2 charge state. On the other hand, most of the other frequency contributions do not participate significantly to the total formation entropy with the only exception of the LA Part 1 contribution which is relatively enhanced compared to the one of the neutral charge state. As explained previously, as it appears that the difference between the relaxation volume of the core region and the total relaxation volume differs significantly between the neutral state and the charge states, large differences in elastic correction are expected leading to more pronounced variation of the formation entropy. Therefore, this might explain the trend observed for the low density region of the phonon density of states whose contribution vary very significantly as a function of the charge state: TA Part 1 contribution increases from 7.4 kB (for the charge state –2) to 18.1 kB for charge state +2 while the LA part 1 contribution varies from 1.6 kB to 7.8 kB. As a result, the formation entropy of the neutral state is the lowest one with
largely exceeding the one of neutral –2 charge state. On the other hand, most of the other frequency contributions do not participate significantly to the total formation entropy with the only exception of the LA Part 1 contribution which is relatively enhanced compared to the one of the neutral charge state. As explained previously, as it appears that the difference between the relaxation volume of the core region and the total relaxation volume differs significantly between the neutral state and the charge states, large differences in elastic correction are expected leading to more pronounced variation of the formation entropy. Therefore, this might explain the trend observed for the low density region of the phonon density of states whose contribution vary very significantly as a function of the charge state: TA Part 1 contribution increases from 7.4 kB (for the charge state –2) to 18.1 kB for charge state +2 while the LA part 1 contribution varies from 1.6 kB to 7.8 kB. As a result, the formation entropy of the neutral state is the lowest one with  with charge state displaying formation entropy sligthly above 9 kB. Finally, one has to keep in mide that the background charge imposed in the DFT calculation so as to reproduce the different charge states is known to be rather problematic when considering volume changes [9, 62]. In such, the total energy of the system is directly related not only to the variation of the electronic states forming the band edges upon the introduction of a mechanical perturbation but also to the electrostatic convention used within the ab initio codes used for the study. Therefore, post treatment is necessary in order to obtain correct formation volume and are probably necessary in the case presented here where modes with large Grüneisen parameters (e.g. LA part 1 and part 2) are disturbed. Bruneval et al. [62] has demonstrated that in the case of the silicon vacancy, the +2 charge state is particularly impacted by such electrostatic effects resulting in a very large difference in relaxation volume when the proper correction is accounted for.
with charge state displaying formation entropy sligthly above 9 kB. Finally, one has to keep in mide that the background charge imposed in the DFT calculation so as to reproduce the different charge states is known to be rather problematic when considering volume changes [9, 62]. In such, the total energy of the system is directly related not only to the variation of the electronic states forming the band edges upon the introduction of a mechanical perturbation but also to the electrostatic convention used within the ab initio codes used for the study. Therefore, post treatment is necessary in order to obtain correct formation volume and are probably necessary in the case presented here where modes with large Grüneisen parameters (e.g. LA part 1 and part 2) are disturbed. Bruneval et al. [62] has demonstrated that in the case of the silicon vacancy, the +2 charge state is particularly impacted by such electrostatic effects resulting in a very large difference in relaxation volume when the proper correction is accounted for.
8 Conclusion
The present study investigates the simple case of vibrational formation entropy of VSi, highlighting the difficulty to compute vibrational formation entropy using first principle techniques within the supercell approach. First of all, the precision of the phonon calculation required in order to obtain accurate formation entropy in the case of the silicon vacancy i silicon, independently of the techniques used (either DFPT or FP have similar drastic convergence requirement) makes the calculation technically gruesome to carry out. Therefore, it is doubtful that brute force calculations of formation entropy of point defect using first principles techniques are of any relevanve to the actual experimental formation entropy. It has emerged from this study that (i) low wave-vector and low frequency acoustic mode needs to be described extremely well as they might contribute significantly to the formation entropy, (ii) large positive value of formation entropy might be related to an enhancement of the DOS in the low frequency region originating from an inaccurate description of acoustic modes or the presence of negative modes, (iii) the use of very small supercells induces important perturbations to the lattice and as a consequence to the resulting phonon spectrum, (iv) a universal elastic correction scheme free of simplistic approximation (as the isotropy of the core region) and possible double counting error is still needed and (v) all frequency and Brillouin zone regions should be sampled uniformly and extremely accurately as strong cross cancellation occurs between contributions from different regions and (vi) anharmonic effects should be also accounted for as their contribution to the formation entropy might be of the same order of magnitude as the total harmonic contribution of the phonons particularly in the case of the presence of soft modes. It also appears that ab initio techniques may not represent a significant and systematic improvement over the use of empirical potentials as depending on their range and types of interactions, empirical potentials may generate sparse interatomic force constant matrix less prone to numerical errors. A possible perspective in calculating highly accurate formation entropy of point defect is to combine both improved integration techniques [65] with high accuracy empirical potentials obtained from first principles techniques as developped in recent years through various fitting procedures [66, 67, 68]. Thereby, it is not sure that the level of accuracy that has been set for this study is sufficient to ensure proper convergence of vibrational formation entropy of VSi as evidenced by the variability of the results as a function of charge states, formalism (constant volume versus zero pressure), numerical expression for the derivation or DFT technicalities (types of functional used).
Acknowledgments
J.V. acknowledges stimulating discussions with Dr H. Levard from Aalto University and Pr. D. Alfè from University College London. This project has been supported by the French Government in the frame of the program of investment for the future (Programme d’Investissement d’Avenir ANR-IEED-002-01).
References
- P.M. Fahey, P. Griffin, J. Plummer, Rev. Mod. Phys. 61, 289 (1989) [Google Scholar]
- C. Persson, Y.J. Zhao, S. Lany, A. Zunger, Phys. Rev. B 72, 035211 (2005) [Google Scholar]
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti, C.G. Van de Walle, Rev. Mod. Phys. 86, 253 (2014) [Google Scholar]
- S. Lany, A. Zunger, Phys. Rev. B 78, 235104 (2008) [Google Scholar]
- A. Alkauskas, P. Deák, J. Neugebauer, A. Pasquarello, C.G. Van de Walle, Advanced Calculations for Defects in Materials: Electronic Structure Methods (John Wiley & Sons, 2011) [Google Scholar]
- A. Stoneham, Theory of Defects in Solids: Electronic Structure of Defects in Insulators and Semiconductors, Oxford classic texts in the physical sciences (Clarendon Press, 2001) [Google Scholar]
- G. Makov, M. Payne, Phys. Rev. B 51, 4014 (1995) [Google Scholar]
- C. Varvenne, F. Bruneval, M.C. Marinica, E. Clouet, Phys. Rev. B 88, 134102 (2013) [Google Scholar]
- F. Bruneval, C. Varvenne, J.P. Crocombette, E. Clouet, Phys. Rev. B 91, 024107 (2015) [Google Scholar]
- H. Peng, D.O. Scanlon, V. Stevanovic, J. Vidal, G.W. Watson, S. Lany, Phys. Rev. B 88, 115201 (2013) [Google Scholar]
- S. Lany, A. Zunger, Phys. Rev. Lett. 98, 045501 (2007) [CrossRef] [PubMed] [Google Scholar]
- A. Kolpak, S. Ismail-Beigi, Phys. Rev. B 83, 165318 (2011) [Google Scholar]
- A. Satta, F. Willaime, S. de Gironcoli, Phys. Rev. B 57, 11184 (1998) [Google Scholar]
- P. Erhart, K. Albe, A. Klein, Phys. Rev. B 73, 205203 (2006) [Google Scholar]
- V. Kosyak, N.B. Mortazavi Amiri, A.V. Postnikov, M.A. Scarpulla, J. Appl. Phys. 114, 124501 (2013) [Google Scholar]
- T. Zacherle, P.C. Schmidt, M. Martin, Phys. Rev. B 87, 235206 (2013) [Google Scholar]
- A.J. Jackson, A. Walsh, Phys. Rev. B 88, 165201 (2013) [Google Scholar]
- M. de Koning, C.R. Miranda, A. Antonelli, Phys. Rev. B 66, 104110 (2002) [Google Scholar]
- Y. Mishin, M.R. Sorensen, A.F. Voter, Philos. Mag. A 81, 2591 (2001) [CrossRef] [Google Scholar]
- O.K. Al-Mushadani, R.J. Needs, Phys. Rev. B 68, 235205 (2003) [Google Scholar]
- A. Sholihun, M. Saito, T. Ohno, T. Yamasaki, Jpn J. Appl. Phys. 54, 041301 (2015) [Google Scholar]
- L. Shi, L.W. Wang, Phys. Rev. Lett. 109, 245501 (2012) [CrossRef] [PubMed] [Google Scholar]
- D. Maroudas, R.A. Brown, Phys. Rev. B 47, 15562 (1993) [Google Scholar]
- S. Chiesa, P.M. Derlet, S.L. Dudarev, Phys. Rev. B 79, 214109 (2009) [Google Scholar]
- S.J. Clark, G.J. Ackland, Phys. Rev. B 48, 10899 (1993) [Google Scholar]
- P.J. Ungar, T. Halicioglu, W.A. Tiller, Phys. Rev. B 50, 7344 (1994) [Google Scholar]
- B. Grabowski, T. Hickel, J. Neugebauer, Phys. Stat. Sol. (b) 248, 1295 (2011) [CrossRef] [Google Scholar]
- A. Glensk, B. Grabowski, T. Hickel, J. Neugebauer, Phys. Rev. X 4, 011018 (2014) [Google Scholar]
- F.H. Stillinger, T.A. Weber, Phys. Rev. B 31, 5262 (1985) [Google Scholar]
- S.E. Taylor, F. Bruneval, Phys. Rev. B 84, 075155 (2011) [Google Scholar]
- E. Rauls, T. Frauenheim, Phys. Rev. B 69, 155213 (2004) [Google Scholar]
- S. Dannefaer, P. Mascher, D. Kerr, Phys. Rev. Lett. 56, 2195 (1986) [CrossRef] [PubMed] [Google Scholar]
- P.E. Blöchl, E. Smargiassi, R. Car, D.B. Laks, W. Andreoni, S.T. Pantelides, Phys. Rev. Lett. 70, 2435 (1993) [CrossRef] [PubMed] [Google Scholar]
- M. Lannoo, G. Allan, Phys. Rev. B 25, 4089 (1982) [Google Scholar]
- M.J. Puska, S. Pöykkö, M. Pesola, R.M. Nieminen, Phys. Rev. B 58, 1318 (1998) [Google Scholar]
- P. Śpiewak, K.J. Kurzydłowski, Phys. Rev. B 88, 195204 (2013) [Google Scholar]
- A.F. Wright, Phys. Rev. B 74, 165116 (2006) [Google Scholar]
- F. Corsetti, A.A. Mostofi, Phys. Rev. B 84, 035209 (2011) [Google Scholar]
- W. Gao, A. Tkatchenko, Phys. Rev. Lett. 111, 045501 (2013) [CrossRef] [PubMed] [Google Scholar]
- G. Watkins, J. Troxell, A. Chatterjee, Defects and radiation effects in semiconductors, 1978 (1979) [Google Scholar]
- J.A. Van Vechten, C.D. Thurmond, Phys. Rev. B 14, 3539 (1976) [Google Scholar]
- S. Baroni, S. de Gironcoli, A. Dal Corso, P. Giannozzi, Rev. Mod. Phys. 73, 515 (2001) [Google Scholar]
- G. Kresse, J. Furthmer, Phys. Rev. B 54, 11169 (1996) [Google Scholar]
- G. Kresse, D. Joubert, Phys. Rev. B 59, 1758 (1999) [Google Scholar]
- D. Alfè, Computer Physics Communications 180, 2622 (2009) [Google Scholar]
- J.P. Perdew, K. Burke, M. Ernzerhof, Phys. Rev. Lett. 77, 3865 (1996) [Google Scholar]
- Y. Okada, Y. Tokumaru, J. Appl. Phys. 56, 314 (1984) [Google Scholar]
- M. Probert, M. Payne, Phys. Rev. B 67, 075204 (2003) [Google Scholar]
- M. Ganchenkova, L. Oikkonen, V. Borodin, S. Nicolaysen, R. Nieminen, Materials Science and Engineering: B 107, 159160 (2009) [Google Scholar]
- G.A. Baraff, E.O. Kane, M. Schlüter, Phys. Rev. B 21, 5662 (1980) [Google Scholar]
- G. Henkelman, B.P. Uberuaga, H. Jónsson, J. Chem. Phys. 113, 9901 (2000) [Google Scholar]
- M.J. Puska, S. Pöykkö, M. Pesola, R.M. Nieminen, Phys. Rev. B 58, 1318 (1998) [Google Scholar]
- J. Van Vechten, Phys. Rev. B 33, 8785 (1986) [Google Scholar]
- U. Gerstmann, E. Rauls, H. Overhof, T. Frauenheim, Phys. Rev. B 65, 195201 (2002) [Google Scholar]
- B. Fultz, Progress in Materials Science 55, 247 (2010) [Google Scholar]
- D.S. Kim, H.L. Smith, J.L. Niedziela, C.W. Li, D.L. Abernathy, B. Fultz, Phys. Rev. B 91, 014307 (2015) [Google Scholar]
- A. Debernardi, S. Baroni, E. Molinari, Phys. Rev. Lett. 75, 1819 (1995) [CrossRef] [PubMed] [Google Scholar]
- A. Debernardi, Phys. Rev. B 57, 12847 (1998) [Google Scholar]
- K. Esfarjani, G. Chen, H.T. Stokes, Phys. Rev. B 84, 085204 (2011) [Google Scholar]
- J. Fernandez, A. Monti, R. Pasianot, Phys. Stat. Sol. (b) 219, 245 (2000) [CrossRef] [Google Scholar]
- S.A. Centoni, B. Sadigh, G.H. Gilmer, T.J. Lenosky, T. Díaz de la Rubia, C.B. Musgrave, Phys. Rev. B 72, 195206 (2005) [Google Scholar]
- F. Bruneval, J.P. Crocombette, Phys. Rev. B 86, 140103 (2012) [Google Scholar]
- S. Wei, M.Y. Chou, Phys. Rev. B 50, 2221 (1994) [Google Scholar]
- G. Ackland, M. Warren, S. Clark, J. Phys.: Condens. Matter 9, 7861 (1997) [CrossRef] [Google Scholar]
- B. Grabowski, L. Ismer, T. Hickel, J. Neugebauer, Phys. Rev. B 79, 134106 (2009) [Google Scholar]
- F. Ercolessi, J.B. Adams, Europhys. Lett. 26, 583 (1994) [Google Scholar]
- S. Hobday, R. Smith, J. Belbruno, Modelling and Simulation in Materials Science and Engineering 7, 397 (1999) [Google Scholar]
- S. Bukkapatnam, M. Malshe, P. Agrawal, L. Raff, R. Komanduri, Phys. Rev. B 74, 224102 (2006) [Google Scholar]
Cite this article as: Pia Seeberger, Julien Vidal, On the ab initio calculation of vibrational formation entropy of point defect: the case of the silicon vacancy, EPJ Photovoltaics 8, 85505 (2017).
All Tables
Found stable defect structures of the neutral and charged silicon vacancy are displayed. Found ground state structures within this study are marked with a bullet • and other authors are referenced. Symmetry-labels are given in Schnflies notation and distances R between the ions neighbouring the vacancy for the 432 atom cell are given in Å. Furthermore total energies Etot, energy differences ΔE and for the neutral vacancy the formation enthalpies ΔHf are displayed.
All Figures
 |
Fig. 1 Formation entropies for the Si vacancy from literature. References are with the first letter of the authors last names and the year the paper was published: SS0Y15 [21], MN03 [20], MB93 [23], CA93 [25], RF07 [31], DMK86 [32], BSCLAP93 [33], LA82 [34]. |
| In the text | |
 |
Fig. 2 Energy profile between different local arrangements of the 1st neighbour atoms surrounding the silicon vacancy. |
| In the text | |
 |
Fig. 3 Integration function (n + 1)ln(n + 1)−nln(n) of equation (2) as a function of frequency for different temperature values. |
| In the text | |
 |
Fig. 4 Phonon density of states of Si obtained from the FP approach for different sizes of supercell calculated using the GGA functional. Experimental data are taken from reference [56]. |
| In the text | |
 |
Fig. 5 Vibrational entropy of Si obtained from the FP approach for different sizes of supercell. Experimental data are taken from reference [56]. |
| In the text | |
 |
Fig. 6 Difference of vibrational entropy for 432 atom perfect supercell considering the normalized phonon DOS obtained from a 432 atom supercell and a 1428 atom supercell. |
| In the text | |
 |
Fig. 7 DOS difference Δg(ω) for neutral defect VSi in the D2d configuration. Black broken line represent the fitting function in the low frequency range. |
| In the text | |
 |
Fig. 8 Frequency contribution to the vibrational formation entropy |
| In the text | |
 |
Fig. 9 Phonon density of states for neutral defect VSi in the Td configuration. The grey filled curve represents the density of states of the perfect lattice for a 1428 atom supercell. |
| In the text | |
 |
Fig. 10 High temperature frequency contribution to the vibrational formation entropy |
| In the text | |
 |
Fig. 11 Phonon density of states for different charge of the defect VSi in their ground state configuration. The grey filled curve represents the density of states of the perfect lattice for a 432 atom supercell. Inset shows the vibrational formation entropy for the different charge states. |
| In the text | |
 |
Fig. 12 Frequency contribution to the vibrational formation entropy |
| In the text | |
 |
Fig. 13 Frequency contribution to the vibrational formation entropy |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


