EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 2 (2011) EPJ Photovolt., 2 (2011) 20301 Full HTML
Open Access
Issue
EPJ Photovolt.
Volume 2, 2011
Article Number 20301
Number of page(s) 6
Section Semiconductor Thin Films
DOI https://doi.org/10.1051/epjpv/2011001
Published online 01 April 2011

© EDP Sciences 2011

Licence Creative Commons This is an Open Access article distributed under the terms of the Creative Commons Attribution-Noncommercial License 3.0, which permits unrestricted use, distribution, and reproduction in any noncommercial medium, provided the original work is properly cited.

1 Introduction

The technological progress that has been made in the development of thin film silicon solar cells has led to a significant reduction in the cost per peak watt generated by such devices. Thin film silicon materials such as hydrogenated amorphous (a-Si:H), polymorphous (pm-Si:H) and microcrystalline silicon (μc-Si:H) have become a serious alternative to monocrystalline silicon for the fabrication of solar cells, as the production cost can be drastically reduced through numerous mechanisms: (i) in contrast to the high temperature process (>1400 °C) used in preparing mono or polycrystalline silicon, the plasma enhanced chemical vapor deposition (PECVD) technique, which is a widely used deposition process to fabricate thin film solar cells, needs relatively low temperatures (<300 °C); (ii) the thin film semiconductor can be deposited directly on low-cost large-area substrates; (iii) high deposition rates combined with low defect density silicon thin films have been obtained using PECVD or other deposition techniques [1, 2, 3, 4] leading to good efficiency solar cells.

To further decrease the cost per watt for thin film devices, a common design strategy is to increase conversion efficiency through the use of multijunction cells. In tandem devices, two PIN cells made with materials of different bandgap energies are fabricated in series [5, 6, 7]. A low bandgap material such as microcrystalline silicon can be used as the bottom cell in conjunction with amorphous silicon (top cell) to extend the spectral range of high collection efficiency [5, 8]. Also used as the top cell in such structures is polymorphous silicon, a nanostructured material deposited by PECVD at high pressure and RF power, in a regime where silicon clusters and nanocrystals synthesized in the plasma contribute to the growth along with silicon radicals [9]. It has been reported in previous studies that pm-Si:H has better electronic properties and stability than conventional a-Si:H [10, 11, 12, 13]. Moreover, the pm-Si:H optical gap being slightly larger than the a-Si:H one, the use of pm-Si:H in a tandem structure in place of a-Si:H allows one the possibility to increase the open-circuit voltage of the entire device and therefore to increase the electric output of the photovoltaic modules.

We present herein a comparative numerical modeling study of two tandem pm-Si:H/μc-Si:H cell structures: (1) a conventional tandem cell for which the two elementary PIN cells are superimposed by successive layer deposition; and (2) an assembly of two electrically decoupled PIN cells. After having introduced the two structures in detail, including the relevant cell parameters, we report on the simulation procedure used to optimize the power delivered by each structure, and finally discuss our results.

2 Technical details

In a conventional tandem device, the two elementary cells are directly stacked by successive layer deposition, which means that they are both optically and electrically coupled [5, 6, 7]. To provide the current to the load, this structure requires only two contact electrodes connected to the top cell P layer and to the bottom cell N layer. In the following, we will call this design the “two-wire structure”. Using this interconnection design, the two cells are physically series connected and thus have the same current flowing through them. This introduces an important constraint, because the thickness of each cell has to be precisely chosen in order to share the same short circuit current. Otherwise, the cell with the higher short circuit current will have to work at a shifted operating point due to the lower current of the other cell. This will lead to a degraded performance compared to the optimal, current-matched situation.

This design requirement leads to the idea of an electrical cell decoupling in order to independently target the maximum power of each cell, the current-matching constraint being released. In this configuration, each cell has its own electrodes connected to its own P and N layers. Thus, the two cells in such a combination are optically coupled and electrically decoupled, and we will refer to this design as a “four-wire structure”. These two tandem cell structures are presented in Figure 1.

We focus here on tandem pm-Si:H/μc-Si:H cells. The pm-Si:H PIN cell needs a small intrinsic layer (i-layer) thickness (several hundreds of nm) to convert its useful spectrum. This property is linked to the high absorption coefficient of this material due to its direct-like band-gap. On the other hand, the μc-Si:H PIN cell requires a thicker i-layer (a few μms) so as to compensate its lower absorption coefficient. In the tandem configuration, the solar spectrum is more used more efficiently, as the top pm-Si:H cell will absorb the energy of photons with less thermalization loss, whereas the bottom μc-Si:H cell will transfer the infrared energy that would normally go unabsorbed.

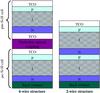thumbnail Fig. 1

Two-wire versus four-wire tandem structures.

In order to quantify the power benefit one can expect from using the four-wire structure instead of the traditional two-wire one, we have used numerical modelling software dedicated to studying heterojunction solar cells, “AFORS-HET” (Automat FOR Simulation of HETerostructures). This software has been developed by the Hahn-Meitner Institut (now Helmholtz Zentrum) in Berlin [14]. Macroscopic characteristics of different layer structures and layer interfaces can be simulated in the dark or under illumination, taking into account optical reflections at any existing interfaces. A different sub-gap defect density spectrum can be introduced for each layer.

In the case of a two-wire structure, the tunnel-recombination effect which occurs at the N(pm-Si:H)/P(μc-Si:H) interface and which allows the passage of current between the two sub-cells is not included in the simulation. Thus, it is well adapted to the simulation of independent individual solar cells (four-wire structure) since the elementary cells are decoupled. For the two-wire structure simulation, we calculated the J-V characteristics of each cell separately, taking into account the optical coupling. The J-V characteristics of the two-wire structure are then reconstructed considering that the current is the same in each sub-cell (fundamental characteristic of a conventional tandem cell). The maximal power can then be calculated and compared to that of the four-wire tandem structure. Note that this procedure neglects the losses that might be due in practice from a non ideal tunnel-recombination between the cells, so the solar cell performance calculated on the two-wire tandem might be somewhat overestimated.

Table 1

Main electrical parameters of the pm-Si:H and μc-Si:H intrinsic layers introduced in the simulation.

Polymorphous silicon and microcrystalline silicon are both characterized by defects in their energy bandgap. Two kinds of defects can be mainly observed: the deep defects linked to the dangling bonds and the network defects linked to the weak bonds.

The first defect category, even if it is known to be of amphoteric type [15, 16], can be modelled by two Gaussian continuous distributions of monovalent states [17]: with a peak value Dmax, peak position Emax and the standard deviation σ0 that depend on the quality of the film (that depends itself on the deposition conditions) as well as on the doping.

The second category is represented by an extension of the valence band and the conduction band on either side of the forbidden band. Those extensions are modelled by two exponential bandtails. The description of the valence bandtail is given by: where EUV is the characteristic energy width of the tail, and GV0 the DOS at the valence band edge. An analogous expression holds for the conduction band tail, with a characteristic energy width EUD.

The material parameters for the μc-Si:H and pm-Si:H cells used in the numerical calculations originate from several references [18, 19, 20, 21]. The main parameters of intrinsic layers introduced in our simulation are given in Table 1.

The refractive index of each layer, from which the absorption and the reflection of the incoming photons according to their wavelength can be calculated, has been derived from spectroscopic ellipsometry measurements. It should be noted that no light scattering due to texturing was used in this study, and therefore the absolute values of current-density for a given layer thickness will be lower than typically observed in devices using textured substrates.

3 Simulation procedure

To optimize the two cells so that the global structure (two- or four-wire structures) can produce the maximum power, it is necessary to tune the thickness of each pm-Si:H and μc-Si:H i-layer. The thickness of the top pm-Si:H cell plays the key role, as it additionally determines the part of the incident photon flux that is transmitted to the bottom μc-Si:H cell. Moreover, in the micromorph tandem a-Si:H/μc-Si:H cell approach, the thickness of the μc-Si:H cell is on the order of several micrometers [7, 22]. However, in order to reduce production costs, one should reduce the thickness of the μc-Si:H layer as much as possible. Therefore, we have decided to fix the thickness of the intrinsic part of the μc-Si:H cell at a reasonable value of 1.5 μm and to sweep the width of the intrinsic pm-Si:H layer. The P and N layers are mainly used to create the junctions and the internal electrical field in the I-layers, and should be kept as thin as possible. We also therefore fixed the thickness of these very thin layers at values that are typical for PIN cells. These values are summarized in Table 2. Moreover, both junctions are sandwiched between two SnO2 transparent electrodes. In order to enhance the photon absorption probability in the bottom cell, the microcrystalline cell is designed with an Ag back reflector.

Table 2

Layer thicknesses for pm-Si:H and μc-Si:H cells as used in simulation.

To define the thickness range of the pm-Si:H intrinsic layer, we took into account the ageing process, which occurs during the first months of solar illumination. Exposure to solar illumination causes the creation of new dangling bonds created by breaking weak bonds, observed as the so-called light-soaking (LS) or Staebler-Wronski effect [23]. The DOS of pm-Si:H after light-soaking was modeled by increasing the magnitude of the dangling bond Gaussian distribution (Dmax). We present in Figure 2 the pm-Si:H cell efficiency as a function of the pm-Si:H layer thickness for different values of Dmax introduced in the simulation.

thumbnail Fig. 2

Pm-Si:H cell efficiency as a function of pm-Si:H intrinsic layer thickness for three values of the Gaussian distribution peak value Dmax (expressed in cm-3 eV-1): 5 × 1015 (■), 1 × 1016 (°) and 1 × 1017 (△).

It can be observed that for a constant i-layer thickness, the cell efficiency deteriorates with an increase in defect density, as caused by the light soaking process, as the DOS increase shortens the charged carriers’ diffusion length. For a given DOS, the efficiency shows an optimum in i-layer thickness due to recombination growing more quickly with thickness than the number of photogenerated electron-hole pairs. This optimal thickness is lowered by an increase of the DOS. In our simulation, this optimal thickness is located beyond 4 μm for a low peak DOS in the pm-Si:H I layer, representative of a cell in the as-deposited state (Dmax = 5 × 1015cm-3 eV-1), then decreases to 2.7 μm after intermediate degradation caused by light-soaking (Dmax = 1 × 1016cm-3 eV-1), and finally stabilizes around 0.5 μm for a fully light-soaked cell (Dmax = 1 × 1017 cm-3 eV-1). We need to take into account this last data which represents the point that will guarantee us the good function of the cell. After several months of utilization, a cell with I-layer more than 500 nm thick would work far less efficiently than one with a thinner I-layer.

To conclude, when thinking of a long term use, the i-layer thickness of the pm-Si:H cell must not exceed 500 nm. This maximal thickness value is even thinner for greater values of the DOS. In this study, our light-soaked cell is described by a Dmax of 1 × 1017cm-3 eV-1, and so the maximal i-layer thickness is chosen as 450 nm. At the opposite side of the sweep range, technological considerations limit the thinnest possible i-layer to 50 nm. Consequently, we have varied the I-layer thickness of the pm-Si:H cell from 50 nm to 450 nm with a step of 50 nm.

Regarding the former results, we have optimized the top cell intrinsic layer thickness in both two- and four-wire structures following the procedure illustrated in Figure 3 for the two-wire cell and in Figure 4 for the four-wire cell.

thumbnail Fig. 3

Simulation steps for a two-wire tandem structure.

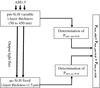thumbnail Fig. 4

Simulation steps for a four-wire tandem structure.

The different steps can be summarized as follows:

  • 1.

    Application of standard AM1.5 illumination at the toppm-Si:H cell.

  • 2.

    Variations of the intrinsic layer thickness from 50 nm to 450 nm with a 50 nm step.

  • 3.

    For each thickness, the output light flux of the pm-Si:H cell is calculated and is used as an input flux of the μc-Si:H cell. J-V and P-V curves are then computed for both cells.

  • 4.

    For the four-wire structure, using the P-V curves, the maximum power is determined by adding the maximum power of elementary cells.

  • 5.

    For the two-wire structure, the output currents have to be matched. So, we first determine the common current range in both cells. We then get for each current density J, the voltage of the global multi-junction structure Vpm − Si:H + Vμc − Si:H. We hence plot the J − (Vpm − Si:H + Vμc − Si:H) and P − (Vpm − Si:H + Vμc − Si:H) curves of the two-wire tandem structure. From this data, we can establish the maximum power of the structure.

4 Results and discussion

We present in this section simulation results for both elementary cells and for both two- and four-wire tandem structures.

The pm-Si:H and μc-Si:H PIN cell simulations allow us to compute the variation in maximum device output power with polymorphous cell i-layer thickness. These variations are plotted in Figure 5 for the thickness range under consideration (50 nm to 450 nm) for the pm-Si:H i-layer. Our initial assumptions are confirmed:

  • for a pm-Si:H cell in the as-deposited (AD) state, the wider theintrinsic layer, the better the efficiency,

  • the LS pm-Si:H cell provides its maximum power for a 300 nm thick intrinsic layer,

  • the μc-Si:H cell maximum power is directly linked to the number of photons coming out of the top pm-Si:H cell. By this simple fact, the thinner the top cell, the more efficient the bottom cell.

As described in Figures 3 and 4, we determined the maximal power of two- and four-wire structures as a function of the pm-Si:H i-layer thickness. These results are presented in Figure 6 in both the AD and LS state.

thumbnail Fig. 5

Maximum output power of elementary cells versus pm-Si:H i-layer thickness.

thumbnail Fig. 6

Maximum output power of both tandem structures as a function of pm-Si:H i-layer thickness (AD and LS state shown).

This figure reveals interesting differences between the two structures. In the case of the as-deposited top pm-Si:H cell, we notice that the four-wire structure is always more efficient, regardless of top cell thickness. The maximum power delivered by the four-wire structure monotonically increases with increasing top cell thickness, as all photons absorbed in the top cell are used more efficiently than those in the bottom cell due to less thermalization loss. No offsetting effect is present due to very low defect density. The two-wire structure must cope with the current matching constraint, so the two-wire structure performance depicts a maximum point around 100 nm as this constraint prevents the pm-Si:H cell from operating at its maximum power point. Under the condition of good pm-Si:H electronic properties, we can draw a 12.6% gain by using the four-wire structure in comparison to the traditional two-wire structure. This gain may be even greater in the case of a thicker top pm-Si:H cell.

In reality, the pm-Si:H cell thickness will be limited by the Staebler-Wronski effect. This is observed for the case of a light-soaked pm-Si:H cell, where the four-wire device output power exhibits a maximum at 200 nm. Again, the absolute value of these numbers will be shifted with respect to actual values, as no light-diffusion by textured substrates is included.

We must also underline that in the four-wire structure, the total device efficiency is more robust with respect to variations of the pm-Si:H thickness. The maximum power fluctuations do not exceed 7.5% for this structure, whereas for the two-wire structure the decrease is more pronounced and reaches 23%. This parametric robustness of the four-wire structure is typical of the fact that even though one cell faces electronic defects, the second one is not modified.

In the light-soaked case, the benefit of using a four-wire structure instead of a two-wire one seems to be small, about 4% for the optimum thickness. But this value may be actually much more important. First, the simulation software does not take into account the tunnel-recombination junction effect which occurs in the N(pmSi:H)/P(μcSi:H) junction and which degrades the two-wire tandem structure performance. Second, all the simulations have been implemented with the standard AM1.5 solar flux whereas the incident solar spectrum is subject to extensive variations due to influences such as incidence angle, cloud cover, etc. These variations influence the power delivered by of each cell and hence make the “current-matching” condition that much more limiting. As shown by the above simulations, the four-wire structure will be much less sensitive to such variations due to the decoupling of the elementary cells.

5 Summary and conclusions

Through numerical simulation, we have performed a comparative study of thin film pm-Si:H/μc-Si:H tandem cells with two different interconnection designs: a conventional, “two-wire” structure where the two PIN cells are superimposed and electrically coupled, and a “four-wire” structure where the two PIN cells are optically coupled but electrically decoupled. The aim of this study was to quantify the output power benefit one can expect from using the four-wire structure instead of the traditional two-wire one. This benefit was studied both before and after material degradation through light soaking.

The results reveal that the four-wire structure is more efficient in both as-deposited and light-soaked state, although the obtained power benefit of the four-wire structure is only 4% when comparing optimized structures in the light-soaked state. However, this benefit may be underestimated, as variations in the photon flux due to outdoor conditions were not modeled. Moreover, we note the robustness of the four-wire design to i-layer thickness variations; its peak output power fluctuations do not exceed 7.5% for the range studied, whereas the thickness effect on the two-wire structure is more pronounced, and results in an output power decrease up to 23%. This may have important consequences regarding robustness to fluctuations during the cell fabrication process.

Acknowledgments

The work was carried out under the project “Association Tandem Optimisée pour le Solaire (ATOS)” supported by “Agence Nationale de la Recherche (ANR)”.

Références

  1. Y.M. Soro, A. Abramov, M.E. Gueunier-Farret, E.V. Johnson, C. Longeaud, P. Roca i Cabarrocas, J.P. Kleider, J. Non-Cryst. Solids 354, 2092 (2008) [CrossRef] [Google Scholar]
  2. A. Matsuda, M. Takai, T. Nishimoto, M. Kondo, Sol. Energy Mater. Sol. Cells 78, 3 (2003) [CrossRef] [Google Scholar]
  3. H. Kakiuchi, M. Matsumoto, Y. Ebata, H. Ohmi, K. Yasutake, K. Yoshii, Y. Mori, J. Non-Cryst. Solids 351, 741 (2005) [CrossRef] [Google Scholar]
  4. A.H. Mahan, Y. Xu, E. Iwaniczko, D.L. Williamson, B.P. Nelson, Q. Wang, J. Non-Cryst. Solids 299–302, 2 (2002) [CrossRef] [Google Scholar]
  5. J. Meier, E. Vallat-Sauvain, S. Dubail, U. Kroll, J. Dubail, S. Golay, L. Feitknecht, P. Torres, S. Fay, D. Fischer, A. Shah, Sol. Energy Mat. Sol. Cells 66, 73 (2001) [Google Scholar]
  6. T. Matsui, H. Jia, M. Kondo, Prog. Photovolt.: Res. Appl. 18, 48 (2010) [Google Scholar]
  7. A.V. Shah, H. Schade, M. Vanecek, J. Meier, E. Vallat-Sauvain, N. Wyrsch, U. Kroll, C. Droz, J. Bailat, Prog. Photovolt.: Res. Appl. 12, 113 (2004) [Google Scholar]
  8. P.D. Veneri, P. Aliberti, L.V. Mercaldo, I. Usatii, C. Privato, Thin Solid Films 516, 6979 (2008) [CrossRef] [Google Scholar]
  9. P. Roca i Cabarrocas, Th. Nguyen-Tran, Y. Djeridane, A. Abramov, E. Johnson, G. Patriarche, J. Phys. D: Appl. Phys. 40, 2258 (2007) [CrossRef] [Google Scholar]
  10. C. Longeaud, J.P. Kleider, P. Roca i Cabarrocas, S. Hamma, R. Meaudre, M. Meaudre, J. Non-Cryst. Solids 227–230, 96 (1998) [CrossRef] [Google Scholar]
  11. R. Butté, R. Meaudre, M. Meaudre, S. Vignoli, C. Longeaud, J.P. Kleider, P. Roca i Cabarrocas, Philos. Mag. B 79, 1079 (1999) [Google Scholar]
  12. M. Meaudre, R. Meaudre, R. Butté, S. Vignoli, C. Longeaud, J.P. Kleider, P. Roca i Cabarrocas, J. Appl. Phys. 86, 946 (1999) [Google Scholar]
  13. J.P. Kleider, C. Longeaud, M. Gauthier, M. Meaudre, R. Meaudre, R. Butté, S. Vignoli, P. Roca i Cabarrocas, Appl. Phys. Lett. 75, 3351 (1999) [Google Scholar]
  14. R. Stangl, A. Froitzheim, M. Kriegel, T. Brammer, S. Kirste, L. Elstner, H. Stiebig, M. Schmidt, W. Fuhs, in Proc. of the 19th Eur. Photovoltaic Solar Energy Conf., 2004, Paris, France, pp. 1497−1500 [Google Scholar]
  15. R.A. Street, N.F. Mott, Phys. Rev. Lett. 35, 1293 (1975) [CrossRef] [Google Scholar]
  16. R.A. Street, K. Winer, Phys. Rev. B 40, 6236 (1989) [CrossRef] [Google Scholar]
  17. J. Meier, U. Kroll, E. Vallat-Sauvain, J. Spitznagel, U. Graf, A. Shah, Sol. Energy 77, 983 (2004) [CrossRef] [Google Scholar]
  18. S. Tchakarov, U. Dutta, P. Roca i Cabarrocas, P. Chatterjee, J. Non-Cryst. Solids 338–340, 766 (2004) [CrossRef] [Google Scholar]
  19. E. Klimovsky, A. Sturiale, F.A. Rubinelli, Thin Solid Films 515, 4826 (2007) [CrossRef] [Google Scholar]
  20. E.V. Johnson, M. Nath, P. Roca i Cabarrocas, A. Abramov, P. Chatterjee, J. Non-Cryst. Solids 354, 2455 (2008) [CrossRef] [Google Scholar]
  21. M. Nath, P. Roca i Cabarrocas, E.V. Johnson, A. Abramov, P. Chatterjee, Thin Solid Films 516, 6974 (2008) [CrossRef] [Google Scholar]
  22. S. Lee, M. Gunes, C.R. Wronsky, N. Maley, M. Bennet, Appl. Phys. Lett. 59, 1578 (1991) [CrossRef] [Google Scholar]
  23. D.L. Staebler, C.R. Wronsky, Appl. Phys. Lett. 31, 292 (1977) [CrossRef] [Google Scholar]

All Tables

Table 1

Main electrical parameters of the pm-Si:H and μc-Si:H intrinsic layers introduced in the simulation.

In the text
Table 2

Layer thicknesses for pm-Si:H and μc-Si:H cells as used in simulation.

In the text

All Figures

thumbnail Fig. 1

Two-wire versus four-wire tandem structures.
In the text
thumbnail Fig. 2

Pm-Si:H cell efficiency as a function of pm-Si:H intrinsic layer thickness for three values of the Gaussian distribution peak value Dmax (expressed in cm-3 eV-1): 5 × 1015 (■), 1 × 1016 (°) and 1 × 1017 (△).
In the text
thumbnail Fig. 3

Simulation steps for a two-wire tandem structure.
In the text
thumbnail Fig. 4

Simulation steps for a four-wire tandem structure.
In the text
thumbnail Fig. 5

Maximum output power of elementary cells versus pm-Si:H i-layer thickness.
In the text
thumbnail Fig. 6

Maximum output power of both tandem structures as a function of pm-Si:H i-layer thickness (AD and LS state shown).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.